题目

给你一个由 X-Y 平面上的点组成的数组 points ，其中 points[i] = [xi, yi] 。从其中取任意三个不同的点组成三角形，返回能组成的最大三角形的面积。与真实值误差在 10-5 内的答案将会视为正确答案**。**

示例 1：

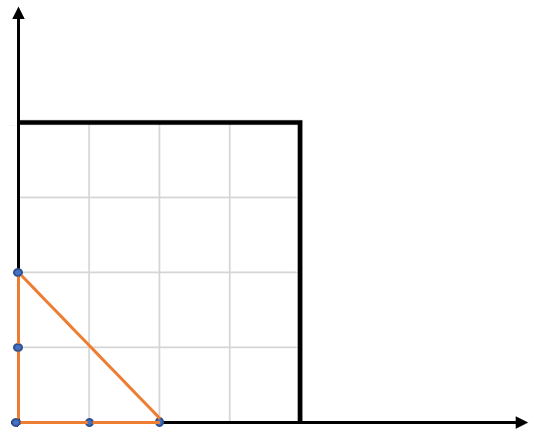
输入：points = [[0,0],[0,1],[1,0],[0,2],[2,0]] 输出：2.00000 解释：输入中的 5 个点如上图所示，红色的三角形面积最大。

示例 2：

输入：points = [[1,0],[0,0],[0,1]] 输出：0.50000

提示：

• 3 <= points.length <= 50
• -50 <= xi, yi <= 50
• 给出的所有点 互不相同

解题思路

求三角形面积有几种非常有效的方法。其中最直接、最适合编程计算的是 “鞋带公式”（Shoelace Formula）。面积的计算公式是： $$\mathrm{Area}=\frac{1}{2}|(x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2))|$$

具体代码

class Solution {
public:
    double largestTriangleArea(vector<vector<int>>& points) {

        int n = points.size();
        double Area = 0.0;
        for(int i = 0; i < n - 2; ++i)
        {
            for(int j = i + 1; j < n - 1; ++j)
            {
                for(int k = j + 1; k < n; ++k)
                {
                    int x1 = points[i][0];
                    int y1 = points[i][1];
                    int x2 = points[j][0];
                    int y2 = points[j][1];
                    int x3 = points[k][0];
                    int y3 = points[k][1];
                    double sum1 = x1 * y2 + x2 * y3 + x3 * y1;
                    double sum2 = y1 * x2 + y2 * x3 + y3 * x1;
                    Area = max(Area, 0.5 * abs(sum1 - sum2));
                }
            }
        }
        
        return Area;
        
    }
};