题目

有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 **“大西洋”**处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

示例 1：

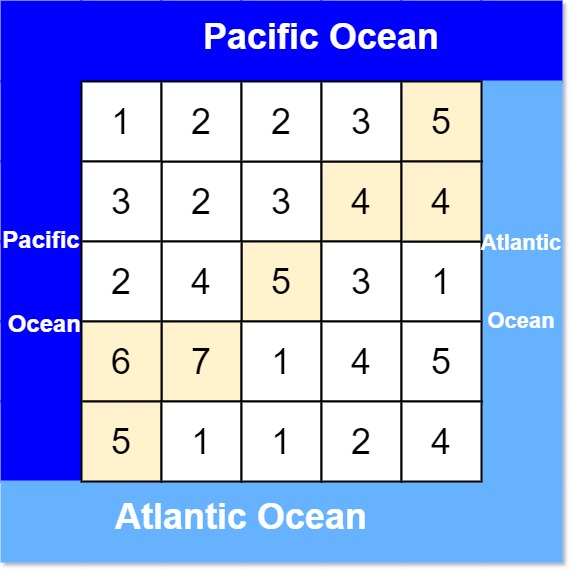
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]] 输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

示例 2：

输入: heights = [[2,1],[1,2]] 输出: [[0,0],[0,1],[1,0],[1,1]]

提示：

m == heights.length
n == heights[r].length
1 <= m, n <= 200
0 <= heights[r][c] <= 10^5

解题思路

问题转换：
- “水从 A 点能流到太平洋” 等价于 “太平洋的水能‘反向流’到 A 点”。
- 水顺流的条件是：从高处流向等于或低于它的地方 (height[next] <= height[current])。
- 那么，水“反向流”的条件就是：从低处流向等于或高于它的地方 (height[next] >= height[current])。
分而治之：我们可以把问题分解成两个子问题：
- 找到所有能流向 太平洋 的单元格。
- 找到所有能流向 大西洋 的单元格。这两个集合的交集就是最终的答案。

详细步骤：

创建两个布尔矩阵：
- 创建一个 can_reach_pacific 矩阵，大小与 heights 相同，用于标记可以流到太平洋的单元格。
- 创建一个 can_reach_atlantic 矩阵，同样大小，用于标记可以流到大西洋的单元格。
从太平洋边界出发进行搜索：
- 太平洋的边界是第 0 行和第 0 列的所有单元格。
- 从所有这些边界单元格开始，进行一次 DFS（或 BFS）遍历。
- 遍历的规则是：只有当下一个单元格的高度 大于或等于 当前单元格的高度时，才能从当前单元格移动到下一个单元格（这就是我们上面说的“反向流”）。
- 将所有在这次遍历中访问到的单元格，在 can_reach_pacific 矩阵中对应位置标记为 true。
从大西洋边界出发进行搜索：
- 大西洋的边界是最后一行和最后一列的所有单元格。
- 同样，从所有这些边界单元格开始，进行一次 DFS（或 BFS）遍历。
- 使用相同的“反向流”规则（height[next] >= height[current]）。
- 将所有在这次遍历中访问到的单元格，在 can_reach_atlantic 矩阵中对应位置标记为 true。
找出最终结果：
- 遍历整个 heights 矩阵。
- 如果一个单元格 (r, c) 在 can_reach_pacific 和 can_reach_atlantic 中都为 true，那么它就是我们想要的答案。将其坐标 [r, c] 添加到最终的结果列表中。

具体代码

// 定义四个方向的移动：上、下、左、右
var dirs = [][]int{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}

func pacificAtlantic(heights [][]int) [][]int {
    // 处理边界情况，如果矩阵为空则直接返回
    if len(heights) == 0 || len(heights[0]) == 0 {
        return [][]int{}
    }

    m, n := len(heights), len(heights[0])

    // 创建两个布尔矩阵，分别记录能到达太平洋和大西洋的单元格
    pacificReachable := make([][]bool, m)
    atlanticReachable := make([][]bool, m)
    for i := range pacificReachable {
        pacificReachable[i] = make([]bool, n)
        atlanticReachable[i] = make([]bool, n)
    }

    // 从太平洋边界（第一行和第一列）开始进行DFS
    for i := 0; i < m; i++ {
        dfs(i, 0, pacificReachable, heights)
    }
    for j := 0; j < n; j++ {
        dfs(0, j, pacificReachable, heights)
    }

    // 从大西洋边界（最后一行和最后一列）开始进行DFS
    for i := 0; i < m; i++ {
        dfs(i, n-1, atlanticReachable, heights)
    }
    for j := 0; j < n; j++ {
        dfs(m-1, j, atlanticReachable, heights)
    }

    // 找出两个可达性矩阵都为true的单元格，即为最终结果
    var result [][]int
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if pacificReachable[i][j] && atlanticReachable[i][j] {
                result = append(result, []int{i, j})
            }
        }
    }

    return result
}

// dfs 函数用于从 (r, c) 开始，标记所有可以 "反向流" 到达的单元格
func dfs(r, c int, visited [][]bool, heights [][]int) {
    // 如果当前单元格已经被访问过，直接返回，防止重复计算
    if visited[r][c] {
        return
    }
    // 标记当前单元格为已访问
    visited[r][c] = true

    m, n := len(heights), len(heights[0])

    // 遍历四个方向
    for _, dir := range dirs {
        newR, newC := r+dir[0], c+dir[1]

        // 检查新坐标是否越界
        if newR < 0 || newR >= m || newC < 0 || newC >= n {
            continue
        }

        // 如果新坐标已经被访问过，则跳过
        if visited[newR][newC] {
            continue
        }

        // 核心条件：只有当邻居的高度大于或等于当前高度时，才能 "反向流" 过去
        if heights[newR][newC] >= heights[r][c] {
            dfs(newR, newC, visited, heights)
        }
    }
}

417. 太平洋大西洋水流问题

beautifulremi

题目

解题思路

具体代码