菜单
文章 Leetcode

407. 接雨水 II

beautifulremi

beautifulremi

• 阅读本文需 8 分钟

题目

给你一个 m x n 的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度，请计算图中形状最多能接多少体积的雨水。

示例 1:

输入: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] 输出: 4 解释: 下雨后，雨水将会被上图蓝色的方块中。总的接雨水量为1+2+1=4。

示例 2:

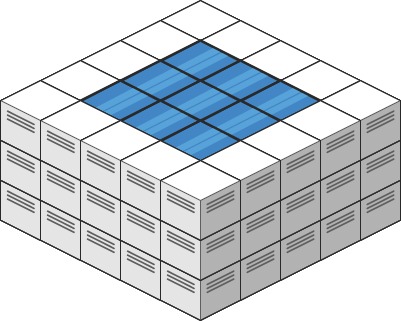
输入: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]] 输出: 10

提示:

  • m == heightMap.length
  • n == heightMap[i].length
  • 1 <= m, n <= 200
  • 0 <= heightMap[i][j] <= 2 * 10^4

解题思路

核心思想是从外向内，逐步确定每个位置能蓄水的“木桶短板”。

我们可以想象一下，雨水最终能否被留住，取决于这个位置周围是否存在一个完整的、比它高的“围墙”。水能蓄多高，则取决于这个“围墙”上最低的那个点（木桶短板效应）。

由于水是从高处往低处流，最外围的一圈单元格是无法蓄水的，因为水会直接流到矩阵外面去。因此，这个外围圈就是我们寻找“围墙”的起点。

这道题最优的解法是 最小堆（优先队列） + 广度优先搜索（BFS）。

  1. 木桶原理
  • 把整个 m x n 的矩阵想象成一个凹凸不平的盆地。
  • 矩阵最外围的一圈格子是盆地的边缘，水可以从这里流走。
  • 内部某个格子 (i, j) 能蓄多少水，不取决于它自己有多高，而是取决于包围它的“围墙”有多高。更准确地说，取决于这圈“围墙”中最矮的那一块。
  1. 从最矮的墙开始

我们的策略是，从已知的“围墙”出发，不断向内部探索，每次都从当前所有围墙中最矮的那个点开始。

因为最矮的墙决定了它旁边区域的蓄水上限。如果我们从一个很高的墙开始，我们可能会错误地认为它旁边可以蓄很多水，但实际上水可能从另一侧一个更矮的墙流走了。

这“每次都从当前集合中找到最小值”的特性，符合最小堆这种数据结构。

  1. 详细步骤
  • 初始化“围墙”:
    • 创建一个最小堆，用于存放 (高度, 行, 列)。这个堆会根据“高度”进行排序，始终保持堆顶是当前所有“围墙”单元格中高度最低的那个。
    • 创建一个 visited 矩阵，用来标记已经处理过的单元格，避免重复计算。
    • 将矩阵最外围一圈的所有单元格加入最小堆，并同时在 visited 矩阵中标记为已访问。因为它们是最初的、已知的“围墙”。
  • 主循环（从最矮的墙向内扩展）:
    • 当最小堆不为空时，循环执行以下操作：
    • a. 取出最矮的墙: 从最小堆中弹出堆顶元素 (h, r, c)。这个 h 就是当前我们找到的、包围着未访问区域的“围墙”中最矮的高度。我们可以称之为 current_wall_height。
    • b. 探索邻居: 查看 (r, c) 的上、下、左、右四个邻居 (nr, nc)。
    • c. 处理邻居: 对于每一个合法的（未越界且未被访问过的）邻居：
      • 计算蓄水: 将邻居的高度 heightMap[nr][nc] 与 current_wall_height (也就是 h) 进行比较。
        • 如果 h > heightMap[nr][nc]，说明邻居比当前的“围墙”矮，水可以被困住。蓄水量就是 h - heightMap[nr][nc]。将这个水量累加到最终结果 total_water 中。
      • 更新“围墙”: 邻居 (nr, nc) 现在也被我们访问了，它成为了新的“围墙”的一部分，需要被加入到最小堆中，以便后续从它这里继续向内探索。
        • 问题是，应该以什么高度将它加入堆中？
        • 如果邻居本身就比 h 高，那么它自己就成了一堵更高的墙，新的墙高就是它自己的高度 heightMap[nr][nc]。
        • 如果邻居比 h 矮，它被水淹没了，水面高度是 h。所以从这个点再向内看，等效的“墙高”也变成了 h。
        • 综合起来，加入堆的高度是 max(h, heightMap[nr][nc])。
      • 标记访问: 在 visited 矩阵中将 (nr, nc) 标记为已访问。
  1. 结束:
    • 当最小堆为空时，说明所有内部的单元格都已经被访问完毕，total_water 就是最终结果。

具体代码

package main

import "container/heap"

// Cell 结构体用于表示地形图中的一个单元格。
type Cell struct {
	height int // 格子的高度
	row    int // 格子所在的行
	col    int // 格子所在的列
}


type PriorityQueue []Cell

func (pq PriorityQueue) Len() int { return len(pq) }

func (pq PriorityQueue) Less(i, j int) bool { return pq[i].height < pq[j].height }

func (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }

func (pq *PriorityQueue) Push(x any) {
	// 我们知道存入的必然是 Cell 类型，所以进行类型断言。
	*pq = append(*pq, x.(Cell))
}

func (pq *PriorityQueue) Pop() any {
	old := *pq
	n := len(old)
	item := old[n-1]
	*pq = old[0 : n-1]
	return item
}

// max 是一个辅助函数，返回两个整数中的较大者。
func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func trapRainWater(heightMap [][]int) int {
	// 边界情况检查：如果地图的行数或列数小于3，它无法形成一个封闭的“容器”，因此无法存水。
	if len(heightMap) < 3 || len(heightMap[0]) < 3 {
		return 0
	}

	m, n := len(heightMap), len(heightMap[0])

	// 使用一个一维切片来模拟二维的 visited 数组。
	visited := make([]bool, m*n)

	// 创建优先队列（最小堆），并初始化。
	pq := make(PriorityQueue, 0)
	heap.Init(&pq)

	// 性能优化：只遍历矩阵的四条边来初始化“围墙”，而不是遍历整个 m*n 矩阵。
	// 这样可以将初始化循环的次数从 m*n 降低到 2*m + 2*n。

	// 1. 处理上下两条边
	for j := 0; j < n; j++ {
		// 上边
		visited[0*n+j] = true
		heap.Push(&pq, Cell{height: heightMap[0][j], row: 0, col: j})
		// 下边
		visited[(m-1)*n+j] = true
		heap.Push(&pq, Cell{height: heightMap[m-1][j], row: m-1, col: j})
	}

	// 2. 处理左右两条边 (注意循环范围 i 从 1 到 m-2，避免重复处理四个角)
	for i := 1; i < m-1; i++ {
		// 左边
		visited[i*n+0] = true
		heap.Push(&pq, Cell{height: heightMap[i][0], row: i, col: 0})
		// 右边
		visited[i*n+(n-1)] = true
		heap.Push(&pq, Cell{height: heightMap[i][n-1], row: i, col: n-1})
	}

	totalWater := 0
	// dirs 定义了向 上、下、左、右 四个方向探索的坐标偏移量。
	dirs := [][]int{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}

	// 主循环：只要“围墙”（优先队列）不为空，就不断从最矮处向内探索。
	for pq.Len() > 0 {
		// 从堆顶弹出一个 Cell，这是当前所有“围墙”格子里高度最低的一个。
		// 这个 cell 的高度决定了它周围低洼区域的蓄水上限（木桶短板效应）。
		cell := heap.Pop(&pq).(Cell)

		// 遍历当前 cell 的四个邻居。
		for _, dir := range dirs {
			nr, nc := cell.row+dir[0], cell.col+dir[1]

			// 检查邻居的有效性：
			// 1. 是否在地图边界内。
			// 2. 是否是之前从未访问过的新格子（使用一维索引访问 visited）。
			if nr >= 0 && nr < m && nc >= 0 && nc < n && !visited[nr*n+nc] {
				// 标记新格子为已访问，防止重复处理。
				visited[nr*n+nc] = true

				// 核心计算逻辑：如果当前“围墙”的高度 > 邻居的地面高度，说明水被挡住了，可以蓄水。
				if cell.height > heightMap[nr][nc] {
					// 蓄水量 = 水位高度 (cell.height) - 地面高度 (heightMap[nr][nc])
					totalWater += cell.height - heightMap[nr][nc]
				}

				// 将这个邻居也加入到“围墙”中，准备下一次探索。
				// 关键点：推入堆中的新“围墙”的高度，必须是它自身高度和当前水位的较大值。
				// 因为如果邻居被水淹了，那么从它这里再向内看时，等效的“墙高”就是当前的水位高度。
				heap.Push(&pq, Cell{height: max(cell.height, heightMap[nr][nc]), row: nr, col: nc})
			}
		}
	}

	return totalWater
}
分享