题目
给你一个大小为 n x m 的二维整数矩阵 grid,其中每个元素的值为 0、1 或 2。
V 形对角线段 定义如下:
- 线段从
1开始。 - 后续元素按照以下无限序列的模式排列:
2, 0, 2, 0, ...。 - 该线段:
- 起始于某个对角方向(左上到右下、右下到左上、右上到左下或左下到右上)。
- 沿着相同的对角方向继续,保持 序列模式 。
- 在保持 序列模式 的前提下,最多允许 一次顺时针 90 度转向 另一个对角方向。
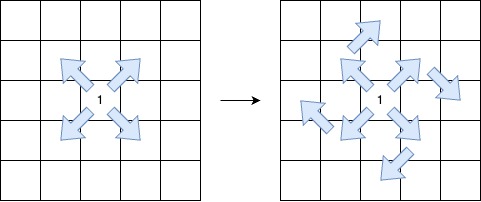
返回最长的 V 形对角线段 的 长度 。如果不存在有效的线段,则返回 0。
示例 1:
输入: grid = [[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]
输出: 5
解释:
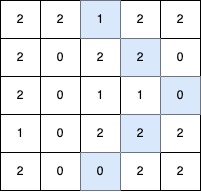
最长的 V 形对角线段长度为 5,路径如下:(0,2) → (1,3) → (2,4),在 (2,4) 处进行 顺时针 90 度转向 ,继续路径为 (3,3) → (4,2)。
示例 2:
输入: grid = [[2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]
输出: 4
解释:
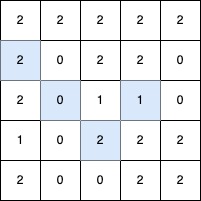
最长的 V 形对角线段长度为 4,路径如下:(2,3) → (3,2),在 (3,2) 处进行 顺时针 90 度转向 ,继续路径为 (2,1) → (1,0)。
示例 3:
输入: grid = [[1,2,2,2,2],[2,2,2,2,0],[2,0,0,0,0],[0,0,2,2,2],[2,0,0,2,0]]
输出: 5
解释:
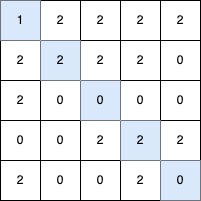
最长的 V 形对角线段长度为 5,路径如下:(0,0) → (1,1) → (2,2) → (3,3) → (4,4)。
示例 4:
输入: grid = [[1]]
输出: 1
解释:
最长的 V 形对角线段长度为 1,路径如下:(0,0)。
提示:
n == grid.lengthm == grid[i].length1 <= n, m <= 500grid[i][j]的值为0、1或2。
具体思路
问题本质分析
首先,这道题的本质是一个寻路和优化问题。我们要在网格中,按照特定规则(对角线移动、数字序列、一次转向)找到一条最长的路径。
看到“最长”、“最优”这类字眼,并且路径的构建具有阶段性(走一步是在前一步的基础上),我们首先想到的最适合的算法思想就是动态规划。
处理“V形”的复杂性
如果题目只要求最长的“直线”对角线段,问题会简单很多。真正的挑战在于“最多允许一次转向”,这引入了“状态”的复杂性。一条路径不仅有长度,还有方向,并且需要“记忆”它是否已经转过弯。
一个简单的 dp[i][j] = “到达(i,j)的最长路径” 是不够的,因为它无法区分路径是从哪个方向来的,也无法知道它是否已经用掉了那次转向机会。
化繁为简
解决这个复杂问题的关键,在于将问题分解成更简单、更容易处理的子问题。
我们可以把“最长的V形对角线段”这个最终目标,拆解为两种情况:
- 最长的直线段(0次转向)。
- 最长的V形段(1次转向)。
最终的答案就是这两种情况里最长的那个。而V形段本身又可以看作是两条直线段的拼接。
这就给了我们一个清晰的解题路线图: 第一步:先解决简单问题,求出所有可能的直线段。 第二步:利用第一步的结果,来构建和计算V形段。
解题步骤
阶段一:计算所有“直线”对角线段
这是我们解题的基础。我们需要知道,从任何一个方向出发,到达网格中任意一点 (i, j) 的最长直线路径有多长。
- 定义状态:我们需要一个DP数组,我们称之为
s(straight的缩写)。s[方向][i][j]记录了沿着某个“方向”,最终在点(i, j)结束的直线段的最大长度。 - 方向划分:对角线有四个方向(左上->右下,右上->左下,左下->右上,右下->左上)。
- 计算方式:
- 对于“向下”走的两个方向(左上->右下,右上->左下),我们可以通过一次从上到下的遍历来计算。因为计算
(i, j)的状态依赖于它上方邻居(i-1, ...)的状态,而这些状态已经被算出来了。 - 对于“向上”走的两个方向,逻辑正好相反,我们需要一次从下到上的遍历来计算。
- 对于“向下”走的两个方向(左上->右下,右上->左下),我们可以通过一次从上到下的遍历来计算。因为计算
- 产出:完成这个阶段后,我们就拥有了四张“地图”(
s[0]到s[3]),详细记录了所有直线段的信息。同时,我们在这个过程中记录下的最大长度,就是“0次转向”情况的答案。
阶段二:构建“V形”对角线段
- V形的本质:一个V形路径,可以看作是在某个点
P进行了一次顺时针转向。它由两部分组成:一个进入点P的直线段(第一段),和一个离开点P的直线段(第二段)。 - 定义状态:我们需要另一个DP数组,称为
v(V-shape的缩写)。v[方向][i][j]记录了这样一个V形路径的最大长度:它的第二段(转向后)沿着“方向”前进,并在点(i, j)结束。 - 计算方式:
- 计算
v[...][i][j]的状态时,它依赖于它相邻点(prev_i, prev_j)的状态。这个状态有两种可能来源:- 延续一个已有的V形:路径从
(prev_i, prev_j)上的一个V形路径直接走过来,方向不变。 - 形成一个新的V形:路径从
(prev_i, prev_j)上的一个直线路径(来自s数组)在这里发生了一次转向。
- 延续一个已有的V形:路径从
- 计算
- 依赖关系:计算
v数组同样需要信息完备的s数组,并且也因为方向问题,需要从上到下和从下到上两次遍历。
具体代码
class Solution {
public:
int lenOfVDiagonal(vector<vector<int>>& grid) {
int n = grid.size();
if (n == 0) return 0;
int m = grid[0].size();
if (m == 0) return 0;
// DP 数组
// s[dir][i][j]: 在 (i,j) 结束的、方向为 dir 的直线段长度
// v[dir][i][j]: 在 (i,j) 结束的、第二段方向为 dir 的 V 形段长度
// 方向 dir: 0:左上->右下(TL->BR), 1:右上->左下(TR->BL), 2:左下->右上(BL->TR), 3:右下->左上(BR->TL)
vector<vector<vector<int>>> s(4, vector<vector<int>>(n, vector<int>(m, 0)));
vector<vector<vector<int>>> v(4, vector<vector<int>>(n, vector<int>(m, 0)));
int maxLen = 0;
// 辅助函数:检查当前值是否能延续一个长度为 prev_len 的路径
auto isValidExtension = [&](int val, int prev_len) {
if (prev_len <= 0) return false;
// 新路径的序列索引为 prev_len (0-indexed)
// 序列: 1(idx 0), 2(idx 1), 0(idx 2), 2(idx 3), ...
if (prev_len % 2 == 1) { // 奇数索引应为 2
return val == 2;
} else { // 偶数索引应为 0
return val == 0;
}
};
// --- 阶段 1: 计算所有直线段 (s 数组) ---
// 正向遍历 (从上到下): 计算方向 0 和 1
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (grid[i][j] == 1) {
s[0][i][j] = 1;
s[1][i][j] = 1;
maxLen = max(maxLen, 1);
} else if (grid[i][j] == 0 || grid[i][j] == 2) {
// 方向 0 (TL -> BR)
if (i > 0 && j > 0 && isValidExtension(grid[i][j], s[0][i - 1][j - 1])) {
s[0][i][j] = s[0][i - 1][j - 1] + 1;
maxLen = max(maxLen, s[0][i][j]);
}
// 方向 1 (TR -> BL)
if (i > 0 && j < m - 1 && isValidExtension(grid[i][j], s[1][i - 1][j + 1])) {
s[1][i][j] = s[1][i - 1][j + 1] + 1;
maxLen = max(maxLen, s[1][i][j]);
}
}
}
}
// 反向遍历 (从下到上): 计算方向 2 和 3
for (int i = n - 1; i >= 0; --i) {
for (int j = 0; j < m; ++j) {
// 【修正】添加对 grid[i][j] == 1 的处理,为从下到上的路径初始化起点
if (grid[i][j] == 1) {
s[2][i][j] = 1;
s[3][i][j] = 1;
} else if (grid[i][j] == 0 || grid[i][j] == 2) {
// 方向 2 (BL -> TR)
if (i < n - 1 && j > 0 && isValidExtension(grid[i][j], s[2][i + 1][j - 1])) {
s[2][i][j] = s[2][i + 1][j - 1] + 1;
maxLen = max(maxLen, s[2][i][j]);
}
// 方向 3 (BR -> TL)
if (i < n - 1 && j < m - 1 && isValidExtension(grid[i][j], s[3][i + 1][j + 1])) {
s[3][i][j] = s[3][i + 1][j + 1] + 1;
maxLen = max(maxLen, s[3][i][j]);
}
}
}
}
// --- 阶段 2: 计算 V 形段 (v 数组) ---
// 正向遍历: 计算 v[0] 和 v[1]
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (grid[i][j] == 0 || grid[i][j] == 2) {
// v[0] (第二段方向: TL -> BR)
if (i > 0 && j > 0) {
if (isValidExtension(grid[i][j], v[0][i - 1][j - 1])) {
v[0][i][j] = max(v[0][i][j], v[0][i - 1][j - 1] + 1);
}
// 转向: 从 s[2] (BL->TR) (2 -> 0)
if (isValidExtension(grid[i][j], s[2][i - 1][j - 1])) {
v[0][i][j] = max(v[0][i][j], s[2][i - 1][j - 1] + 1);
}
if (v[0][i][j] > 0) maxLen = max(maxLen, v[0][i][j]);
}
// v[1] (第二段方向: TR -> BL)
if (i > 0 && j < m - 1) {
if (isValidExtension(grid[i][j], v[1][i - 1][j + 1])) {
v[1][i][j] = max(v[1][i][j], v[1][i - 1][j + 1] + 1);
}
// 转向: 从 s[0] (TL->BR) (0 -> 1)
if (isValidExtension(grid[i][j], s[0][i - 1][j + 1])) {
v[1][i][j] = max(v[1][i][j], s[0][i - 1][j + 1] + 1);
}
if (v[1][i][j] > 0) maxLen = max(maxLen, v[1][i][j]);
}
}
}
}
// 反向遍历: 计算 v[2] 和 v[3]
for (int i = n - 1; i >= 0; --i) {
for (int j = 0; j < m; ++j) {
if (grid[i][j] == 0 || grid[i][j] == 2) {
// v[2] (第二段方向: BL -> TR)
if (i < n - 1 && j > 0) {
if (isValidExtension(grid[i][j], v[2][i + 1][j - 1])) {
v[2][i][j] = max(v[2][i][j], v[2][i + 1][j - 1] + 1);
}
// 转向: 从 s[3] (BR->TL) (3 -> 2)
if (isValidExtension(grid[i][j], s[3][i + 1][j - 1])) {
v[2][i][j] = max(v[2][i][j], s[3][i + 1][j - 1] + 1);
}
if (v[2][i][j] > 0) maxLen = max(maxLen, v[2][i][j]);
}
// v[3] (第二段方向: BR -> TL)
if (i < n - 1 && j < m - 1) {
if (isValidExtension(grid[i][j], v[3][i + 1][j + 1])) {
v[3][i][j] = max(v[3][i][j], v[3][i + 1][j + 1] + 1);
}
// 转向: 从 s[1] (TR->BL) (1 -> 3)
if (isValidExtension(grid[i][j], s[1][i + 1][j + 1])) {
v[3][i][j] = max(v[3][i][j], s[1][i + 1][j + 1] + 1);
}
if (v[3][i][j] > 0) maxLen = max(maxLen, v[3][i][j]);
}
}
}
}
return maxLen;
}
};
