题目

给你一个二维整数数组 squares ，其中 squares[i] = [xi, yi, li] 表示一个与 x 轴平行的正方形的左下角坐标和正方形的边长。

找到一个最小的 y 坐标，它对应一条水平线，该线需要满足它以上正方形的总面积 等于 该线以下正方形的总面积。

答案如果与实际答案的误差在 10-5 以内，将视为正确答案。

注意：正方形 可能会 重叠。重叠区域应该被 多次计数 。

示例 1：

输入： squares = [[0,0,1],[2,2,1]]

输出： 1.00000

解释：

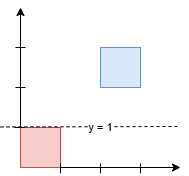
任何在 y = 1 和 y = 2 之间的水平线都会有 1 平方单位的面积在其上方，1 平方单位的面积在其下方。最小的 y 坐标是 1。

示例 2：

输入： squares = [[0,0,2],[1,1,1]]

输出： 1.16667

解释：

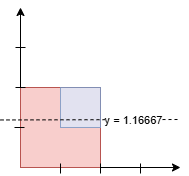
面积如下：

• 线下的面积：7/6 * 2 (红色) + 1/6 (蓝色) = 15/6 = 2.5。
• 线上的面积：5/6 * 2 (红色) + 5/6 (蓝色) = 15/6 = 2.5。

由于线以上和线以下的面积相等，输出为 7/6 = 1.16667。

提示：

• 1 <= squares.length <= 5 * 10^4
• squares[i] = [x_i, y_i, l_i]
• squares[i].length == 3
• 0 <= xi, yi <= 10^9
• 1 <= li <= 10^9
• 所有正方形的总面积不超过 10^12。

解题思路

这道题的关键在于理解题目中关于“面积”的定义和性质：

1. 单调性：随着水平线 $y$ 的坐标从下往上移动（$y$ 增大），该线下方的正方形总面积是非递减的（只会增加或保持不变）。
2. 重叠处理：题目明确说明“重叠区域应该被多次计数”。这意味着我们不需要处理复杂的几何并集（Union）计算，只需要简单地将每个正方形在 $y$ 线以下的部分面积相加即可。

基于以上两点，我们可以将问题转化为：

寻找最小的 $y$，使得 $f(y) \ge \frac{\text{所有正方形的总面积}}{2}$。

其中 $f(y)$ 是 $y$ 线以下所有正方形截取部分的面积之和。

由于 $f(y)$ 是单调的，我们可以使用二分查找来逼近这个 $y$ 值。

1. 计算总面积

遍历所有正方形，计算 $l_i^2$ 的总和，记为 total_area。我们的目标是找到一条线，使得下方的面积至少为 total_area / 2。

2. 确定二分查找的范围

• 下界 (low)：所有正方形中最小的 $y$ 坐标（或者简单地设为 0，因为坐标非负）。
• 上界 (high)：所有正方形中最大的顶部坐标（$y + l$），即 $\max(y_i + l_i)$。

3. 定义 check(y) 函数

这个函数用于计算给定水平线 $y$ 下方的总面积：

对于数组中的每一个正方形 $[x_i, y_i, l_i]$：

• 完全在下方：如果正方形的顶部 $y_i + l_i \le y$，则该正方形贡献面积 $l_i^2$。
• 完全在上方：如果正方形的底部 $y_i \ge y$，则该正方形贡献面积 $0$。
• 被线穿过：如果 $y_i < y < y_i + l_i$，说明线横切了正方形。此时正方形在下方的部分是一个矩形，高度为 $y - y_i$，宽度为 $l_i$。贡献面积 $l_i \times (y - y_i)$。

将所有贡献累加，返回总和。

4. 执行二分查找

由于我们需要的是浮点数答案，二分查找通常有两种终止条件写法：

1. 固定次数循环：循环 60 到 100 次。对于 $10^9$ 的范围，100 次循环可以将精度控制在极小的范围内，远超 $10^{-5}$ 的要求。这是处理浮点二分最稳妥的方法。
2. 精度判断：while (high - low > 1e-7)。

二分逻辑：

• 令 mid = (low + high) / 2。
• 如果 check(mid) >= total_area / 2：
  • 说明当前的 $y$ 已经让下方积累了足够的面积。
  • 因为我们要找最小的 $y$，所以尝试往低处找，令 high = mid。
• 否则：
  • 说明下方积攒的面积还不够，需要往高处找，令 low = mid。

最终 high（或 low）即为答案。

具体代码

func separateSquares(squares [][]int) float64 {
    var totalArea float64
    var low, high float64 = -1, -1

    // 1. 计算总面积，并确定二分查找的上下界
    for _, sq := range squares {
        y := float64(sq[1])
        l := float64(sq[2])
        
        totalArea += l * l
        
        // 初始化或更新下界
        if low == -1 || y < low {
            low = y
        }
        // 初始化或更新上界
        if high == -1 || y+l > high {
            high = y + l
        }
    }

    target := totalArea / 2.0

    // 2. 二分查找
    // 循环 100 次，对于 10^9 的范围，精度远超 10^-5
    // 这比使用 while(high - low > 1e-5) 更稳健
    for i := 0; i < 100; i++ {
        mid := (low + high) / 2
        
        if getAreaBelow(squares, mid) >= target {
            high = mid // 下方积累的面积够了，尝试降低 y 找最小解
        } else {
            low = mid  // 下方面积不够，必须提高 y
        }
    }

    return high
}

// 辅助函数：计算水平线 y 下方的所有正方形面积之和
func getAreaBelow(squares [][]int, yLine float64) float64 {
    var area float64
    for _, sq := range squares {
        y := float64(sq[1])
        l := float64(sq[2])
        
        if yLine <= y {
            // 情况 A: 线在正方形下方，无贡献
            continue
        } else if yLine >= y+l {
            // 情况 B: 线在正方形上方，贡献整个正方形面积
            area += l * l
        } else {
            // 情况 C: 线穿过正方形，贡献部分矩形面积
            // 宽度 * (线的高度 - 正方形底部高度)
            area += l * (yLine - y)
        }
    }
    return area
}