菜单
文章 Leetcode

3446. 按对角线进行矩阵排序

beautifulremi

beautifulremi

• 阅读本文需 8 分钟

题目

给你一个大小为 n x n 的整数方阵 grid。返回一个经过如下调整的矩阵：

  • 左下角三角形（包括中间对角线）的对角线按 非递增顺序 排序。
  • 右上角三角形 的对角线按 非递减顺序 排序。

示例 1：

输入： grid = [[1,7,3],[9,8,2],[4,5,6]]

输出： [[8,2,3],[9,6,7],[4,5,1]]

解释：

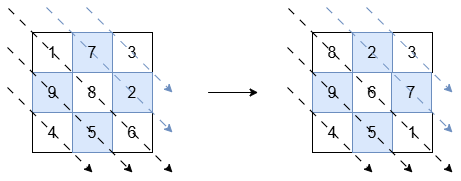
标有黑色箭头的对角线（左下角三角形）应按非递增顺序排序：

  • [1, 8, 6] 变为 [8, 6, 1]。
  • [9, 5] 和 [4] 保持不变。

标有蓝色箭头的对角线（右上角三角形）应按非递减顺序排序：

  • [7, 2] 变为 [2, 7]。
  • [3] 保持不变。

示例 2：

输入： grid = [[0,1],[1,2]]

输出： [[2,1],[1,0]]

解释：

标有黑色箭头的对角线必须按非递增顺序排序，因此 [0, 2] 变为 [2, 0]。其他对角线已经符合要求。

示例 3：

输入： grid = [[1]]

输出： [[1]]

解释：

只有一个元素的对角线已经符合要求，因此无需修改。

提示：

  • grid.length == grid[i].length == n
  • 1 <= n <= 10
  • -10^5 <= grid[i][j] <= 10^5

具体思路

题目要求

题目的核心要求是对矩阵的所有对角线进行排序，但有两套不同的排序规则。要解决这个问题，我们首先需要一个方法来唯一地识别和隔离出每一条对角线。

观察一个方阵的坐标 (i, j)（i是行，j是列），我们可以发现一个关键规律： 所有在同一条“从左上到右下”方向的对角线上的元素，其坐标的差 i - j 的值是恒定的。

这个差值 k = i - j 就像是每条对角线的“身份证号”（ID），我们可以用它来区分不同的对角线。

示例 (3x3 矩阵):

  • 主对角线 (0,0), (1,1), (2,2) -> i - j 始终为 0。
  • 它下方的一条对角线 (1,0), (2,1) -> i - j 始终为 1。
  • 它上方的一条对角线 (0,1), (1,2) -> i - j 始终为 -1。

将规律与排序规则关联

题目将矩阵分为两个区域，对应两种排序规则：

  1. 左下角三角形（含主对角线）：非递增（降序）排序。
  2. 右上角三角形：非递减（升序）排序。

现在，我们将这个区域划分与我们的对角线ID k = i - j 关联起来：

  • 在左下角及主对角线上，行号 i 总是大于或等于列号 j (i >= j)。这意味着 i - j >= 0，所以 k >= 0 的对角线都需要降序排序。
  • 在右上角，行号 i 总是小于列号 j (i < j)。这意味着 i - j < 0，所以 k < 0 的对角线都需要升序排序。

至此，我们已经建立了一个清晰的逻辑：通过判断对角线ID k 的正负，就可以确定其排序规则。

设计高效的算法流程

一个初步的想法可能是将整个矩阵的所有元素都提取出来，存入一个辅助数据结构（比如一个map或者vector<vector>），排序后再放回去。但这样做需要 $O(n^2)$ 的额外空间来存储整个矩阵的副本，并且数据拷贝次数很多。

我们可以构思一个更优的方案：“逐个击破”，即一次只处理一条对角线。 这样做可以极大地降低空间复杂度和数据移动量。

这个优化思路的算法流程如下：

  1. 外层循环：我们不遍历矩阵的 (i, j) 坐标，而是直接遍历所有可能的对角线ID k。k 的范围是从最右上角的 -(n-1) 到最左下角的 n-1。
  2. 内层操作（针对每一条对角线 k）:
    • a. 提取 (Extract)：创建一个临时的、一维的 vector，专门用来存放当前这条对角线 k 上的所有元素。要做到这一点，我们需要找到这条对角线的起点，并沿着它走到终点。
    • b. 排序 (Sort)：对这个临时 vector 进行排序。根据 k 的正负来决定是升序还是降序。
    • c. 写回 (Update)：再次从这条对角线的起点开始，沿着相同的路径，将临时 vector 中排好序的元素依次写回到矩阵 grid 的正确位置。

第四步：解决关键子问题：如何遍历指定的对角线？

上述流程的核心技术点在于：给定一个对角线ID k，如何找到它的起始坐标 (start_row, start_col)？

我们通过分析起点位置的规律来解决它：

  • 对于主对角线及下方的对角线 (k >= 0)，它们的起点一定在矩阵的第一列（col = 0）。根据 k = i - j，我们有 k = start_row - 0，因此 start_row = k。起点为 (k, 0)。
  • 对于主对角线上方的对角线 (k < 0)，它们的起点一定在矩阵的第一行（row = 0）。根据 k = i - j，我们有 k = 0 - start_col，因此 start_col = -k。起点为 (0, -k)。

我们可以用一个统一的公式来表示这个起点：

  • start_row = max(0, k)
  • start_col = max(0, -k)

找到了起点 (r, c) 后，我们只需不断地同时增加行和列（r++, c++），就可以遍历完这条对角线上的所有格子，直到 r 或 c 超出矩阵边界 n。

实现

  1. 确定对角线标识：使用 k = i - j 作为对角线的唯一ID。
  2. 设计主循环：循环遍历所有可能的 k 值，从 -(n-1) 到 n-1，确保覆盖所有对角线。
  3. 为每条对角线执行：
    • 提取：通过 (start_row, start_col) 公式找到起点，遍历对角线，将其元素存入一个临时 vector。
    • 排序：检查 k 的正负，对临时 vector 执行相应的升序或降序排序。
    • 写回：再次遍历该对角线，将排好序的元素从临时 vector 按顺序放回原矩阵。

复杂度分析

时间复杂度：$O(n^2logn)$

  1. 外层循环：代码的主循环遍历了所有的 2n - 1 条对角线。
  2. 内层操作：对于每一条长度为 d 的对角线，主要操作有三步：
    • 提取元素：遍历该对角线，耗时 $O(d)$。
    • 排序：对包含 d 个元素的临时 vector 进行排序，耗时 $O(dlogd)$。
    • 写回元素：再次遍历该对角线，耗时 $O(d)$。
  3. 综合分析：
    • 在这三步中，排序是主要的时间开销，即 $O(dlogd)$。
    • 总时间复杂度是所有对角线排序时间之和：$∑O(d_k​logd_k​)$，其中 $d_k$​ 是第 k 条对角线的长度。
    • 矩阵中所有元素的总数是 $n^2$（即 $∑d_k​=n^2$），最长的对角线长度为 n。
    • 因此，总时间复杂度的上界可以估算为 $O(n^2logn)$。

空间复杂度：O(n)

  1. 主要开销：该算法最大的优点在于空间效率。它不是一次性将所有 n^2 个元素都加载到新内存中。
  2. 临时存储：在处理任何一条对角线时，程序会创建一个临时的 vector<int> 来存储该对角线上的元素。
  3. 峰值空间：这个临时 vector 的最大尺寸取决于最长对角线的长度。在 n x n 矩阵中，最长的对角线是主对角线，其长度为 n。
  4. 结论：因此，算法在任何时刻所需要的额外空间峰值都由这个最长的临时向量决定，即 $O(n)$。

具体代码

class Solution {
public:
    vector<vector<int>> sortMatrix(vector<vector<int>>& grid) {
        if (grid.empty() || grid[0].empty()) {
            return grid;
        }
        int n = grid.size();

        // 遍历所有 2*n - 1 条对角线
        // 对角线 ID k = i - j, 范围从 -(n-1) 到 (n-1)
        for (int k = -(n - 1); k <= n - 1; ++k) {
            
            // 1. 提取对角线元素
            vector<int> temp_diagonal;
            int start_row = max(0, k); // 对角线的起始行
            int start_col = max(0, -k); // 对角线的起始列
            for (int r = start_row, c = start_col; r < n && c < n; ++r, ++c) {
                temp_diagonal.push_back(grid[r][c]);
            }
            
            // 2. 根据规则排序
            if (k >= 0) { // 左下部分，降序
                sort(temp_diagonal.begin(), temp_diagonal.end(), greater<int>());
            } else { // 右上部分，升序
                sort(temp_diagonal.begin(), temp_diagonal.end());
            }

            // 3. 将排序后的元素写回原矩阵
            int current = 0;
            for (int r = start_row, c = start_col; r < n && c < n; ++r, ++c) {
                grid[r][c] = temp_diagonal[current++];
            }
        }
        
        return grid;
    }
};
分享