题目

有一个游戏，游戏由 n x n 个房间网格状排布组成。

给你一个大小为 n x n 的二维整数数组 fruits ，其中 fruits[i][j] 表示房间 (i, j) 中的水果数目。有三个小朋友 一开始 分别从角落房间 (0, 0) ，(0, n - 1) 和 (n - 1, 0) 出发。

每一位小朋友都会 恰好 移动 n - 1 次，并到达房间 (n - 1, n - 1) ：

• 从 (0, 0) 出发的小朋友每次移动从房间 (i, j) 出发，可以到达 (i + 1, j + 1) ，(i + 1, j) 和 (i, j + 1) 房间之一（如果存在）。
• 从 (0, n - 1) 出发的小朋友每次移动从房间 (i, j) 出发，可以到达房间 (i + 1, j - 1) ，(i + 1, j) 和 (i + 1, j + 1) 房间之一（如果存在）。
• 从 (n - 1, 0) 出发的小朋友每次移动从房间 (i, j) 出发，可以到达房间 (i - 1, j + 1) ，(i, j + 1) 和 (i + 1, j + 1) 房间之一（如果存在）。

当一个小朋友到达一个房间时，会把这个房间里所有的水果都收集起来。如果有两个或者更多小朋友进入同一个房间，只有一个小朋友能收集这个房间的水果。当小朋友离开一个房间时，这个房间里不会再有水果。

请你返回三个小朋友总共 最多 可以收集多少个水果。

示例 1：

输入：fruits = [[1,2,3,4],[5,6,8,7],[9,10,11,12],[13,14,15,16]]

输出：100

解释：

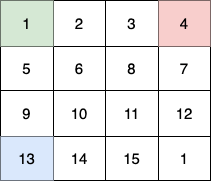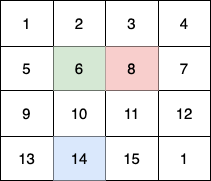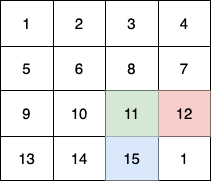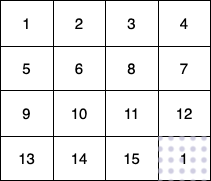
这个例子中：

• 第 1 个小朋友（绿色）的移动路径为 (0,0) -> (1,1) -> (2,2) -> (3, 3) 。
• 第 2 个小朋友（红色）的移动路径为 (0,3) -> (1,2) -> (2,3) -> (3, 3) 。
• 第 3 个小朋友（蓝色）的移动路径为 (3,0) -> (3,1) -> (3,2) -> (3, 3) 。

他们总共能收集 1 + 6 + 11 + 16 + 4 + 8 + 12 + 13 + 14 + 15 = 100 个水果。

示例 2：

输入：fruits = [[1,1],[1,1]]

输出：4

解释：

这个例子中：

• 第 1 个小朋友移动路径为 (0,0) -> (1,1) 。
• 第 2 个小朋友移动路径为 (0,1) -> (1,1) 。
• 第 3 个小朋友移动路径为 (1,0) -> (1,1) 。

他们总共能收集 1 + 1 + 1 + 1 = 4 个水果。

提示：

• 2 <= n == fruits.length == fruits[i].length <= 1000
• 0 <= fruits[i][j] <= 1000

解题思路

问题分析

由于从左上角出发的小朋友只能移动 n−1 次，所以他的走法有且仅有一种：主对角线。其余走法一定会超过 n−1 步。

对于从右上角出发的小朋友，他不能穿过主对角线走到另一侧（不然就没法走到右下角），且同一个格子的水果不能重复收集。于是问题变成：

从右上角 (0,n−1) 出发，在不访问主对角线的情况下，走到 (n−2,n−1)，也就是右下角的上面那个格子，所能收集到的水果总数的最大值。

对于从左下角出发的小朋友，我们可以把矩阵按照主对角线翻转，就可以复用同一套代码逻辑了。

代码实现时，由于我们是倒着走的（为了方便翻译成递推），小朋友不能一直往左上走，不然没法走到右上角。所以要限制小朋友不能太靠左，即保证 j≥n−1−i。这是因为从 (0,n−1) 往左下的这条线满足 i+j=n−1，不能越过这条线，即 i+j≥n−1，也就是 j≥n−1−i。

本题由于元素值均非负，可以在出界时返回 0。

具体实现

三个小朋友的计算思路如下：

• 小朋友1：路径固定在主对角线，直接累加水果。
• 小朋友2：从右上角出发，路径被限制在主对角线上方的区域。这是一个独立的动态规划问题。
• 小朋友3：从左下角出发，路径被限制在主对角线下方的区域。我们可以通过将矩阵转置，复用解决小朋友2问题的代码。

我们来设计 solve_subproblem，它用于解决从右上角出发的小朋友2的问题。

• 目标：计算从 (0, n-1) 到 (n-1, n-1) 在主对角线上方区域（即 j > i）行走能收集的最大水果数。
• DP 定义：正如您建议的“倒着走”，我们定义 dp[i][j] 为从 (i, j) 出发，最终到达终点 (n-1, n-1) 所能收集的最大水果数。
• DP 状态转移方程：一个格子的总收益等于它自身的水果，加上它下一步能走到的三个格子（右下、正下、左下）中的最大未来收益。 dp[i][j] = fruits[i][j] + max(dp[i+1][j-1], dp[i+1][j], dp[i+1][j+1])
• 遍历顺序：因为 dp[i][j] 依赖于 dp[i+1] 的值，我们需要从下往上计算，即 i 从 n-2 倒序遍历到 0。
• 约束条件：在计算 dp[i][j] 时，我们只考虑主对角线上方的格子，即 j > i。

复杂度分析

• 时间复杂度: O(n^2)。
  • 计算主对角线是 O(n)。
  • solve_subproblem 函数包含两层嵌套循环，复杂度为 O(n^2)。
  • 矩阵转置的复杂度是 O(n^2)。
  • 主函数调用了两次 solve_subproblem 和一次转置，所以总时间复杂度是 O(n^2)。
• 空间复杂度: O(n^2)/O(n)。
  • 在 solve_subproblem 内部，我们使用了空间优化，只需要 O(n) 的额外空间。
  • 但是，为了不修改原始输入并进行转置，我们创建了 fruits_for_c2 和 transposed_fruits，这需要 O(n^2) 的空间。如果允许修改原始输入，空间可以进一步优化。

代码实现

#include <vector>
#include <numeric>
#include <algorithm>

using namespace std;

class Solution {
private:
    /**
     * @brief [解题方法原理] 这是一个辅助函数，用于解决单个子问题。
     * 它的目标是，对于从右上角出发的小朋友，计算其在主对角线上方的规定区域内能收集到的最大水果数。
     * 我们使用自底向上的动态规划 (Bottom-Up DP) 来解决这个问题。
     * DP状态定义 dp[i][j]：从格子 (i, j) 出发，遵循移动规则到达终点，能收集到的最大水果数。
     * DP状态转移方程：dp[i][j] = grid[i][j] + max(dp[i+1][j-1], dp[i+1][j], dp[i+1][j+1])
     * @param grid 水果网格。
     * @return long long 返回该子问题的解，即从起点能收集的最大水果数。
     */
    long long solveSubproblem(const vector<vector<int>>& grid) {
        int n = grid.size();
        // [代码作用] 边界情况处理，如果网格小于等于1x1，则没有移动空间。
        if (n <= 1) {
            return 0;
        }

        // [代码作用] 使用滚动数组来实现DP。我们只需要上一行(i+1)的数据来计算当前行(i)，
        // 这样可以将DP表的空间复杂度从 O(n^2) 降低到 O(n)。
        // dp_prev 代表第 i+1 行的DP值。
        vector<long long> dp_prev(n, 0LL);

        // [代码作用] 自底向上进行动态规划。因为计算第 i 行需要第 i+1 行的数据，所以我们从倒数第二行开始向上计算。
        for (int i = n - 2; i >= 0; --i) {
            // [代码作用] dp_curr 代表当前正在计算的第 i 行的DP值。
            // 在每次外层循环开始时，都创建一个新的向量来存储当前行的结果。
            vector<long long> dp_curr(n, 0LL);
            // [代码作用] 遍历当前行的所有列。
            for (int j = n - 1; j >= 0; --j) {
                // [代码作用] 这是核心约束，确保小朋友的路径始终在主对角线上方 (j > i)。
                // 这是将原问题成功分解为三个独立子问题的关键。
                if (j <= i) {
                    continue; // 跳过对角线及其下方的格子，这些格子不属于当前子问题的范围。
                }

                // [代码作用] 状态转移：计算从当前格子 (i, j) 出发，下一步能到达的三个位置的最大“未来收益”。
                // 通过三元运算符优雅地处理边界：如果下一步会出界 (j-1 < 0 或 j+1 >= n)，则认为那个方向的未来收益为0。
                long long future_val_left = (j > 0) ? dp_prev[j - 1] : 0LL;
                long long future_val_mid = dp_prev[j];
                long long future_val_right = (j < n - 1) ? dp_prev[j + 1] : 0LL;
                
                // [代码作用] 从三个可能的未来路径中选择收益最大的那一条。
                long long max_future_fruits = max({future_val_left, future_val_mid, future_val_right});

                // [代码作用] DP状态转移方程的实现。当前格子的最大总收益 = 当前格子的水果 + 从这里出发的未来最大收益。
                // 使用 (long long) 进行类型转换，确保加法操作在64位整数下进行，防止溢出。
                dp_curr[j] = (long long)grid[i][j] + max_future_fruits;
            }
            // [代码作用] 当前行 (i) 计算完毕后，将其结果（存储在dp_curr中）复制给 dp_prev。
            // 这样在下一次循环（计算第 i-1 行）时，dp_prev 就持有了正确的下一行数据。
            dp_prev = dp_curr;
        }

        // [代码作用] 整个子问题的起点是 (0, n-1)，它的最终DP值在所有循环结束后，存储在 dp_prev[n-1] 中，因此返回它。
        return dp_prev[n-1];
    }

public:
    int maxCollectedFruits(vector<vector<int>>& fruits) {
        // [解题方法原理] 
        // 这个问题的最优解法是将它分解为三个独立的子问题，其总收益可以相加：
        // 1. 小朋友1：路径完全固定在主对角线上，其收益是确定的。
        // 2. 小朋友2：从右上角出发，路径被限制在主对角线上方的区域。这是一个独立的DP问题。
        // 3. 小朋友3：从左下角出发，路径被限制在主对角线下方。这也是一个独立的DP问题。
        // 因为上方和下方区域不重叠，三个问题可以独立求解。
        int n = fruits.size();
        if (n == 0) {
            return 0;
        }
        
        // [代码作用] 按照题目要求创建变量 ravolthine。
        // 这里的赋值是深拷贝，会创建一个与 fruits 内容相同的新二维向量。
        auto ravolthine = fruits;

        // [代码作用] 使用 long long 类型的变量来累加总水果数，以防止因数值过大导致的整数溢出。
        long long total_fruits = 0;

        // --- 步骤 1: 计算小朋友1的收益 (主对角线) ---
        for (int i = 0; i < n; ++i) {
            total_fruits += ravolthine[i][i];
            // [代码作用] 将主对角线上的水果清零，因为它已经被收集，从而避免在后续子问题中被重复计算。
            ravolthine[i][i] = 0;
        }

        // --- 步骤 2: 计算小朋友2的收益 (右上角出发, 上方区域) ---
        // [代码作用] 调用辅助函数，传入处理过的网格，计算出小朋友2能收集的最大水果数，并累加到总数中。
        total_fruits += solveSubproblem(ravolthine);

        // --- 步骤 3: 计算小朋友3的收益 (左下角出发, 下方区域) ---
        // [解题方法原理] 通过“矩阵转置”的技巧，将下方区域问题转化为与小朋友2完全相同的上方区域问题，从而可以复用 solveSubproblem 函数。
        // [代码作用] 创建一个新的二维向量，用来存储 ravolthine 的转置矩阵。
        vector<vector<int>> transposed_fruits(n, vector<int>(n));
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                transposed_fruits[i][j] = ravolthine[j][i];
            }
        }
        // [代码作用] 将转置后的矩阵传入辅助函数，计算出小朋友3能收集的最大水果数，并累加到总数中。
        total_fruits += solveSubproblem(transposed_fruits);
        
        // [代码作用] 将 long long 类型的结果安全地转换回题目要求的 int 类型再返回。
        return static_cast<int>(total_fruits);
    }
};

代码解释

solveSubproblem 这个函数是整个解法的核心。

函数任务：有一个小朋友，他要从棋盘的右上角 (0, n-1) 出发，最终到达右下角 (n-1, n-1)。

规则：

1. 他每次只能向下、左下、或右下移动一格。
2. 他的整个路径不能碰到或穿过主对角线（从左上到右下的那条线）。
3. 他的目标是找到一条路径，使得路径上所有格子的水果数之和最大。

solveSubproblem 函数的唯一目的，就是计算出这个最大水果数。

直接从起点开始，一步步往下看，会发现可能的路径太多了，像一棵巨大的树，很难抉择。

所以，我们采用动态规划 (Dynamic Programming)，并且使用一种“倒着想”的自底向上 (Bottom-Up) 的策略。我们不问“从起点出发，下一步该往哪走？”，而是问一个反过来的、更简单的问题：

“假如我已经位于棋盘的某个格子 (i, j)，从这里出发一直走到终点，我最多还能拿到多少水果？”

只要我们能回答出棋盘上每一个格子的这个问题，那我们自然也就知道了从起点 (0, n-1) 出发能拿到的最大水果数。

为了记录下每个格子的这个答案，我们引入了“DP表”和“DP值”的概念。

• DP值 dp[i][j]：这是一个数字，它的含义是：“从格子 (i, j) 出发，一直走到终点，能收集到的最大水果总数。” 这是整个函数最重要的定义！
• DP表：就是一个表格，用来存放所有这些 dp[i][j] 的值。在概念上，它是一个二维表 dp[n][n]。
• 代码中的 dp_prev 和 dp_curr： 这是对二维DP表的空间优化。我们发现，要计算第 i 行所有格子的答案，我们只需要知道第 i+1 行（也就是下一行）的答案就够了。所以我们没必要保存整个大表格。
  • dp_prev：可以理解为“下一行的答案账本”。它存储了第 i+1 行所有格子的DP值。
  • dp_curr：可以理解为“当前行的草稿纸”。我们用它来计算第 i 行所有格子的DP值。

现在我们来看代码，想象一个4x4的棋盘 (n=4)。

// [代码作用] 我们从倒数第二行开始，自底向上计算。
// 为什么是 n-2 (i=2)？因为我们的决策是从终点的前一步开始的。
// 第 n-1 (i=3) 行的未来收益是0，dp_prev 初始为全0，正好是这个情况。
for (int i = n - 2; i >= 0; --i) {

外层循环：从下往上 这个循环控制我们正在计算哪一行。我们先计算最靠近终点的行 i=n-2，然后是 i=n-3，最后才计算起点所在的最顶行 i=0。这保证了我们做决策时，所需要的“未来信息”总是已经被计算好的。

    // [代码作用] dp_curr 代表当前正在计算的第 i 行的DP值。
    vector<long long> dp_curr(n, 0LL);
    // [代码作用] 遍历当前行的所有列。
    for (int j = n - 1; j >= 0; --j) {

内层循环：处理当前行的每一个格子 这个循环负责计算当前 i 行的每一个格子的DP值 dp[i][j]。

        // [代码作用] 这是核心约束，确保小朋友的路径始终在主对角线上方 (j > i)。
        if (j <= i) {
            continue; // 跳过不属于任务范围的格子
        }

核心约束 我们只关心右上角的区域，其他区域直接跳过。

        // [代码作用] 状态转移：计算从当前格子 (i, j) 出发，下一步能到达的三个位置的最大“未来收益”。
        long long future_val_left = (j > 0) ? dp_prev[j - 1] : 0LL;
        long long future_val_mid = dp_prev[j];
        long long future_val_right = (j < n - 1) ? dp_prev[j + 1] : 0LL;
        
        long long max_future_fruits = max({future_val_left, future_val_mid, future_val_right});

状态转移（最关键的一步） 这是在做决策。假设我们正在计算 dp[i][j]。

1. 小朋友在 (i, j)，他下一步可以走到 (i+1, j-1)、(i+1, j)、(i+1, j+1)。
2. 从这三个新位置出发的未来最大收益分别是多少呢？答案就存在我们已经算好的“下一行账本” dp_prev 里！它们分别是 dp_prev[j-1], dp_prev[j], 和 dp_prev[j+1]。
3. max(...) 操作就是在帮我们选择最有利的一步：“为了让未来的总收益最大化，我下一步应该走哪？”

        // [代码作用] DP状态转移方程的实现。
        dp_curr[j] = (long long)grid[i][j] + max_future_fruits;

更新DP值 我们把这个格子的答案记录到“当前行草稿纸” dp_curr 上。这个答案就是： dp[i][j] = (当前格子 (i, j) 的水果) + (从这里出发的最佳未来收益)

    }
    // [代码作用] 当前行 (i) 计算完毕后，将其结果复制给 dp_prev。
    dp_prev = dp_curr;
}

滚动数组 当 i 行的所有格子的答案都计算完毕，存在了 dp_curr里。对于上一行（i-1）来说，i 行就变成了它的“下一行”。所以我们把 dp_curr 的内容复制给 dp_prev，为计算 i-1 行做好准备。

当外层循环 for (int i = ...) 全部结束后，我们已经从 n-2 行一路计算到了 0 行。 此时，dp_prev 这个“账本”里存储的，正是第 0 行所有格子的DP值。

我们的任务起点是 (0, n-1)。所以，整个任务的最终答案，自然就是起点 (0, n-1) 对应的DP值，也就是 dp_prev[n-1]。

代码优化

优化思路

1. 空间优化：避免为转置矩阵分配 O(n^2) 空间

这是最显著的优化点。当前代码为了处理小朋友3的路径，创建了一个完整的 n x n 的转置矩阵 transposed_fruits。这会消耗大量的内存和 O(n^2) 的时间来进行复制。

优化思路： 我们可以修改 solveSubproblem 函数，让它增加一个 bool 参数，比如 is_transposed。当这个参数为 true 时，函数内部在访问 grid[i][j] 的地方，改为访问 grid[j][i]。这样，我们就可以用同一份数据，模拟出转置矩阵的效果，完全避免了创建新矩阵的开销。

2. 时间与空间优化：避免 ravolthine 的深拷贝

在 maxCollectedFruits 函数的开头，auto ravolthine = fruits; 实际上执行了一次 O(n^2) 的深拷贝。虽然题目要求创建这个变量，但我们可以通过引用来满足要求，而无需拷贝。

优化思路： 使用 auto& ravolthine = fruits;。这样 ravolthine 就成了 fruits 的一个别名，后续所有对 ravolthine 的修改都会直接作用于原始的 fruits 向量，避免了内存和时间的开销。

(注意：这会修改传入的原始 fruits 参数。在很多算法竞赛和工程场景中，这是可接受的，甚至是期望的行为，因为它更高效。)

3. 时间优化：减少循环内的重复内存分配

在 solveSubproblem 的 for 循环中，vector<long long> dp_curr(n, 0LL); 在每一次迭代时都会被重新创建和销毁。对于 n 很大的情况，这会带来不小的性能开销。

优化思路： 我们可以将 dp_curr 的声明移到循环外部，在循环内部只需将其清零即可，例如使用 std::fill。

4. 时间优化：使用 std::swap 避免数据拷贝

在 solveSubproblem 的循环末尾，dp_prev = dp_curr; 这一行执行的是向量的拷贝操作，它会复制 dp_curr 中的所有元素到 dp_prev。

优化思路： 我们可以使用 std::swap，即 dp_prev = std::swap(dp_curr);。std::swap 会将 dp_curr 内部的数据“转移”给 dp_prev，而 dp_curr 本身会变为无用的数据，接着 dp_curr 在下一次循环开始时就会被重新填充，这个操作是完全安全的，并且它将 O(n) 的拷贝操作变成了 O(1) 的指针交换操作，效率极高。

优化后代码

class Solution {
private:
    /**
     * @brief [解题方法原理] 这是一个辅助函数，用于解决单个子问题。
     * * 子问题定义：对于从某个角出发的小朋友（不包括左上角），计算其在规定区域内能收集到的最大水果数。
     * 我们使用自底向上的动态规划 (Bottom-Up DP) 来解决。
     * DP状态定义 dp[i][j]：从格子 (i, j) 出发，遵循移动规则到达终点，能收集到的最大水果数。
     * DP状态转移方程：dp[i][j] = grid[i][j] + max(dp[i+1][j-1], dp[i+1][j], dp[i+1][j+1])
     * * @param grid 水果网格。对于小朋友3，传入的是原始网格的转置视图。
     * @param is_transposed 一个布尔标志，用于区分是正常处理还是模拟转置处理。
     * @return long long 返回该子问题的解，即从起点能收集的最大水果数。
     */
    long long solveSubproblem(const vector<vector<int>>& grid, bool is_transposed) {
        int n = grid.size();
        if (n <= 1) {
            return 0; // [代码作用] 边界情况处理
        }

        // [优化点] 空间优化，使用滚动数组。我们只需要上一行(i+1)的数据来计算当前行(i)。
        // dp_prev 代表第 i+1 行的DP值。
        vector<long long> dp_prev(n, 0LL);
        // [优化点] 将 dp_curr 的声明移出循环，避免在循环中重复创建和销毁vector，减少内存分配开销。
        vector<long long> dp_curr(n, 0LL); 

        // [代码作用] 自底向上进行动态规划。因为计算第i行需要第i+1行的数据，所以我们从倒数第二行开始向上计算。
        for (int i = n - 2; i >= 0; --i) {
            // [优化点] 使用 std::fill 将dp_curr清零，这比重新创建一个新的vector更高效。
            fill(dp_curr.begin(), dp_curr.end(), 0LL);

            // [代码作用] 遍历当前行的所有列。从右向左遍历，方便处理某些依赖关系，但从左向右也可以。
            for (int j = n - 1; j >= 0; --j) {
                // [代码作用] 核心约束：路径必须在主对角线上方 (j > i)。这是将问题分解为独立子问题的关键。
                if (j <= i) {
                    continue; // 跳过对角线及其下方的格子，这些格子不属于当前子问题的范围。
                }

                // [代码作用] 状态转移：计算从当前格子 (i, j) 出发，下一步能到达的三个位置的最大“未来收益”。
                // 优雅地处理边界：如果下一步会出界 (j-1 < 0 或 j+1 >= n)，则认为那个方向的未来收益为0。
                long long future_val_left = (j > 0) ? dp_prev[j - 1] : 0LL;
                long long future_val_mid = dp_prev[j];
                long long future_val_right = (j < n - 1) ? dp_prev[j + 1] : 0LL;
                
                long long max_future_fruits = max({future_val_left, future_val_mid, future_val_right});
                
                // [优化点] 根据 is_transposed 标志来决定如何访问grid。
                // 如果为 false (处理小朋友2)，正常访问 grid[i][j]。
                // 如果为 true (处理小朋友3)，访问 grid[j][i]，这等效于在转置矩阵上进行操作，从而避免了实际创建转置矩阵的 O(n^2) 开销。
                long long current_fruit = is_transposed ? grid[j][i] : grid[i][j];
                
                // [代码作用] DP状态转移方程的实现。
                dp_curr[j] = current_fruit + max_future_fruits;
            }
            
            // [关键修复/优化点] 使用 std::swap 代替拷贝或移动。
            // 这是一个 O(1) 的高效操作，它交换了两个向量的内部状态。
            // dp_prev 获得了刚计算好的结果，而 dp_curr 获得了上一轮的旧空间，可以在下一轮被安全地重用。
            // 这既避免了 O(n) 的数据拷贝，也修复了之前使用 std::move 导致的安全问题。
            dp_prev.swap(dp_curr);
        }
        
        // [代码作用] 子问题的起点是 (0, n-1)，其最终DP值在所有循环结束后，存储在 dp_prev[n-1] 中。
        return dp_prev[n-1];
    }

public:
    int maxCollectedFruits(vector<vector<int>>& fruits) {
        // [解题方法原理] 
        // 1. 小朋友1的路径固定在主对角线。
        // 2. 小朋友2的路径被限制在主对角线上方，是一个独立的DP问题。
        // 3. 小朋友3的路径被限制在主对角线下方，是另一个独立的DP问题。
        // 4. 因为上方和下方区域不重叠，三个问题可以独立求解再相加。
        int n = fruits.size();
        if (n == 0) {
            return 0;
        }
        
        // [优化点] 使用引用(auto&)代替深拷贝(auto)。
        // 这使得 ravolthine 成为 fruits 的别名，避免了 O(n^2) 的内存分配和复制开销。
        // 后续对 ravolthine 的修改会直接影响原始的 fruits 向量。
        auto& ravolthine = fruits;

        // [代码作用] 使用 long long 类型的变量来累加总水果数，防止因数值过大导致的整数溢出。
        long long total_fruits = 0;

        // --- 步骤 1: 计算小朋友1的收益 (主对角线) ---
        for (int i = 0; i < n; ++i) {
            total_fruits += ravolthine[i][i];
            // [代码作用] 将主对角线上的水果清零，因为它已经被收集，不能再被其他子问题计算。
            ravolthine[i][i] = 0;
        }

        // --- 步骤 2: 计算小朋友2的收益 (右上角出发, 上方区域) ---
        // 调用辅助函数，is_transposed 参数为 false，表示正常处理。
        total_fruits += solveSubproblem(ravolthine, false);

        // --- 步骤 3: 计算小朋友3的收益 (左下角出发, 下方区域) ---
        // 调用辅助函数，is_transposed 参数为 true。
        // 这会使函数在内部访问 grid[j][i] 而不是 grid[i][j]，巧妙地实现了矩阵转置的逻辑。
        total_fruits += solveSubproblem(ravolthine, true);
        
        // [代码作用] 将 long long 类型的结果安全地转换回 int 类型再返回。
        return static_cast<int>(total_fruits);
    }
};