题目

给你一个二维 二进制 数组 grid。你需要找到 3 个 不重叠、面积非零、边在水平方向和竖直方向上的矩形，并且满足 grid 中所有的 1 都在这些矩形的内部。

返回这些矩形面积之和的最小可能值。

注意，这些矩形可以相接。

示例 1：

输入： grid = [[1,0,1],[1,1,1]]

输出： 5

解释：

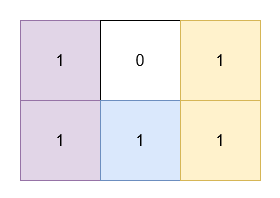
位于 (0, 0) 和 (1, 0) 的 1 被一个面积为 2 的矩形覆盖。
位于 (0, 2) 和 (1, 2) 的 1 被一个面积为 2 的矩形覆盖。
位于 (1, 1) 的 1 被一个面积为 1 的矩形覆盖。

示例 2：

输入： grid = [[1,0,1,0],[0,1,0,1]]

输出： 5

解释：

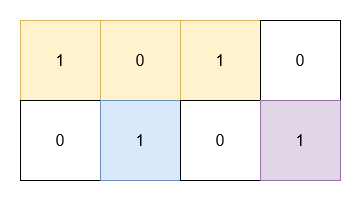
位于 (0, 0) 和 (0, 2) 的 1 被一个面积为 3 的矩形覆盖。
位于 (1, 1) 的 1 被一个面积为 1 的矩形覆盖。
位于 (1, 3) 的 1 被一个面积为 1 的矩形覆盖。

提示：

1 <= grid.length, grid[i].length <= 30
grid[i][j] 是 0 或 1。
输入保证 grid 中至少有三个 1 。

解题思路

由于题目要求将所有1用三个不重叠的矩形覆盖，我们可以把这个复杂问题分解为几个更小的子问题。

我们可以通过两次切割将整个网格划分为三个不重叠的区域。这两次切割可以是水平的，也可以是垂直的，或者是一次水平一次垂直。

这道题的规模（30 * 30）提示我们，可能需要一个动态规划或枚举的解法。考虑到切割方式的有限性，我们可以枚举所有可能的切割位置。

整个思路可以概括为以下步骤：

找到所有1的边界：首先，找到所有1构成的最小外接矩形。这样可以缩小搜索范围，只关注包含所有1的最小区域，从而优化性能。我们可以找出所有1中最小的行索引 min_r，最大的行索引 max_r，最小的列索引 min_c，和最大的列索引 max_c。
枚举切割方式：将网格划分为三个不重叠矩形，总共有六种基本的切割方式。对于每一种切割方式，我们都尝试所有可能的切割位置。
- 三种垂直切割方式：
  1. 两刀都是垂直切割：网格被竖直地切成三块。我们可以枚举第一刀的切割位置 c1（从 min_c 到 max_c），和第二刀的切割位置 c2（从 c1 + 1 到 max_c）。
    - 切割1: 将网格分为 [min_c, c1] 和 [c1+1, max_c] 两部分。
    - 切割2: 将 [c1+1, max_c] 再分为 [c1+1, c2] 和 [c2+1, max_c] 两部分。
    - 对于这三块区域，分别计算覆盖其中所有1所需的最小矩形面积。
- 三种水平切割方式：
  1. 两刀都是水平切割：网格被水平地切成三块。我们可以枚举第一刀的切割位置 r1（从 min_r 到 max_r），和第二刀的切割位置 r2（从 r1 + 1 到 max_r）。
    - 切割1: 将网格分为 [min_r, r1] 和 [r1+1, max_r] 两部分。
    - 切割2: 将 [r1+1, max_r] 再分为 [r1+1, r2] 和 [r2+1, max_r] 两部分。
    - 同样，分别计算三块区域的最小矩形面积。
- 两种混合切割方式：
  1. 一刀垂直，一刀水平：网格首先被垂直地切成两块，然后其中一块再被水平地切成两块。
    - 情况A: 垂直切割在 c1，然后左边区域 [min_c, c1] 被水平切割。
    - 情况B: 垂直切割在 c1，然后右边区域 [c1+1, max_c] 被水平切割。
    - 同理，反过来：一刀水平，一刀垂直，也有两种情况。
计算子矩形的面积：对于每次切割，我们将原始问题分解为三个子问题：在给定区域内，找到一个最小矩形，使其包含该区域内的所有1。这个子问题是简单的：
- 遍历指定区域内的所有单元格，找到所有1的最小和最大行、列索引。
- 如果该区域内没有1，则面积为0。
- 否则，面积 = (max_r - min_r + 1) * (max_c - min_c + 1)。
求和并更新最小值：将这三个子矩形的面积相加，得到当前切割方式下的总面积。将这个总面积与当前的全局最小面积进行比较，并更新最小值。
返回结果：遍历完所有可能的切割方式后，返回得到的全局最小总面积。

为了简化代码，我们可以实现一个辅助函数 solve(r1, c1, r2, c2)，该函数的功能是在由 (r1, c1) 和 (r2, c2) 构成的矩形区域内，找到所有1构成的最小外接矩形的面积。如果该区域内没有1，则返回一个很大的值。

主函数中，通过嵌套循环来枚举所有可能的切割点，并调用 solve 函数三次来计算每个子矩形的面积。

代码实现

class Solution {
private:
    // 辅助函数：计算给定矩形区域内所有 1 的最小外接矩形面积
    int getArea(const vector<vector<int>>& grid, int r1, int c1, int r2, int c2) {
        int min_r = numeric_limits<int>::max(), max_r = numeric_limits<int>::min();
        int min_c = numeric_limits<int>::max(), max_c = numeric_limits<int>::min();
        bool found_one = false;

        for (int r = r1; r <= r2; ++r) {
            for (int c = c1; c <= c2; ++c) {
                if (grid[r][c] == 1) {
                    found_one = true;
                    min_r = min(min_r, r);
                    max_r = max(max_r, r);
                    min_c = min(min_c, c);
                    max_c = max(max_c, c);
                }
            }
        }

        if (!found_one) {
            return 0;
        }

        return (max_r - min_r + 1) * (max_c - min_c + 1);
    }

public:
    int minimumSum(vector<vector<int>>& grid) {
        int R = grid.size();
        int C = grid[0].size();
        int ans = numeric_limits<int>::max();

        // 1. 两次垂直切割
        for (int c1 = 0; c1 < C - 1; ++c1) {
            for (int c2 = c1 + 1; c2 < C - 1; ++c2) {
                int area1 = getArea(grid, 0, 0, R - 1, c1);
                int area2 = getArea(grid, 0, c1 + 1, R - 1, c2);
                int area3 = getArea(grid, 0, c2 + 1, R - 1, C - 1);
                if (area1 > 0 && area2 > 0 && area3 > 0) {
                    ans = min(ans, area1 + area2 + area3);
                }
            }
        }

        // 2. 两次水平切割
        for (int r1 = 0; r1 < R - 1; ++r1) {
            for (int r2 = r1 + 1; r2 < R - 1; ++r2) {
                int area1 = getArea(grid, 0, 0, r1, C - 1);
                int area2 = getArea(grid, r1 + 1, 0, r2, C - 1);
                int area3 = getArea(grid, r2 + 1, 0, R - 1, C - 1);
                if (area1 > 0 && area2 > 0 && area3 > 0) {
                    ans = min(ans, area1 + area2 + area3);
                }
            }
        }

        // 3. 第一次垂直切割，第二次水平切割
        // 情况 A: 左边部分被水平切割
        for (int c = 0; c < C - 1; ++c) {
            int area1 = getArea(grid, 0, c + 1, R - 1, C - 1); // 右边区域
            for (int r = 0; r < R - 1; ++r) {
                int area2 = getArea(grid, 0, 0, r, c);      // 左上区域
                int area3 = getArea(grid, r + 1, 0, R - 1, c); // 左下区域
                if (area1 > 0 && area2 > 0 && area3 > 0) {
                    ans = min(ans, area1 + area2 + area3);
                }
            }
        }

        // 情况 B: 右边部分被水平切割
        for (int c = 0; c < C - 1; ++c) {
            int area1 = getArea(grid, 0, 0, R - 1, c); // 左边区域
            for (int r = 0; r < R - 1; ++r) {
                int area2 = getArea(grid, 0, c + 1, r, C - 1);      // 右上区域
                int area3 = getArea(grid, r + 1, c + 1, R - 1, C - 1); // 右下区域
                if (area1 > 0 && area2 > 0 && area3 > 0) {
                    ans = min(ans, area1 + area2 + area3);
                }
            }
        }

        // 4. 第一次水平切割，第二次垂直切割
        // 情况 C: 上面部分被垂直切割
        for (int r = 0; r < R - 1; ++r) {
            int area1 = getArea(grid, r + 1, 0, R - 1, C - 1); // 下方区域
            for (int c = 0; c < C - 1; ++c) {
                int area2 = getArea(grid, 0, 0, r, c);      // 左上区域
                int area3 = getArea(grid, 0, c + 1, r, C - 1); // 右上区域
                if (area1 > 0 && area2 > 0 && area3 > 0) {
                    ans = min(ans, area1 + area2 + area3);
                }
            }
        }

        // 情况 D: 下面部分被垂直切割
        for (int r = 0; r < R - 1; ++r) {
            int area1 = getArea(grid, 0, 0, r, C - 1); // 上方区域
            for (int c = 0; c < C - 1; ++c) {
                int area2 = getArea(grid, r + 1, 0, R - 1, c);      // 左下区域
                int area3 = getArea(grid, r + 1, c + 1, R - 1, C - 1); // 右下区域
                if (area1 > 0 && area2 > 0 && area3 > 0) {
                    ans = min(ans, area1 + area2 + area3);
                }
            }
        }
        
        return ans;
    }
};

优化思路

如果不改变算法的总体结构（即保持穷举），我们可以优化 getArea 函数，减少它的重复计算。

观察原始代码，getArea(grid, r1, c1, r2, c2) 函数在每次循环中都重新扫描整个子网格，这导致了大量的重复工作。例如，当在遍历两次垂直切割时，c2 的每次变化都会重新计算 c1 左侧的区域。

一个简单的优化是：

缓存结果: 我们可以用一个哈希表或四维数组来存储 getArea 已经计算过的结果，避免对相同子网格的重复计算（尽管在当前的循环结构中，这种重复并不多）。
增量式计算: 在主循环中，我们可以利用前一次迭代的结果来快速计算当前迭代的面积，而不是每次都从头扫描。

我们来分析一下两种混合切割的情况（一次垂直切割，一次水平切割），这是优化空间最大的地方：

第一次垂直切割在 c，第二次水平切割在 r：
- 情况 A：左边区域被水平切割为 [0, r] x [0, c] 和 [r+1, R-1] x [0, c]，右边是完整的 [0, R-1] x [c+1, C-1]。
- 在我们的循环中，外层是 for (int c = 0; c < C - 1; ++c)，内层是 for (int r = 0; r < R - 1; ++r)。
- 在 r 的内层循环中，area3 = getArea(..., c+1, ...) 始终是相同的，因为它只依赖于 c。我们可以把它提出来，避免在 r 的循环中重复计算。
- 同时，area1 和 area2 每次都需要重新计算，因为它们依赖于 r。
第一次水平切割在 r，第二次垂直切割在 c：
- 情况 C：上面区域被垂直切割为 [0, r] x [0, c] 和 [0, r] x [c+1, C-1]，下面是完整的 [r+1, R-1] x [0, C-1]。
- 循环中，外层是 for (int r = 0; r < R - 1; ++r)，内层是 for (int c = 0; c < C - 1; ++c)。
- area3 = getArea(..., r+1, ...) 始终是相同的，我们可以把它提出来，避免在 c 的循环中重复计算。

通过这种方式，我们避免了在一个循环中重复计算不随该循环变量变化的 getArea。这虽然不能改变总体的渐近时间复杂度，但能显著减少实际的计算次数。

优化后代码

class Solution {
private:
    // 辅助函数：计算给定矩形区域内所有 1 的最小外接矩形面积
    int getArea(const vector<vector<int>>& grid, int r1, int c1, int r2, int c2) {
        int min_r = numeric_limits<int>::max(), max_r = numeric_limits<int>::min();
        int min_c = numeric_limits<int>::max(), max_c = numeric_limits<int>::min();
        bool found_one = false;

        for (int r = r1; r <= r2; ++r) {
            for (int c = c1; c <= c2; ++c) {
                if (grid[r][c] == 1) {
                    found_one = true;
                    min_r = min(min_r, r);
                    max_r = max(max_r, r);
                    min_c = min(min_c, c);
                    max_c = max(max_c, c);
                }
            }
        }

        if (!found_one) {
            return 0;
        }

        return (max_r - min_r + 1) * (max_c - min_c + 1);
    }

public:
    int minimumSum(vector<vector<int>>& grid) {
        int R = grid.size();
        int C = grid[0].size();
        int ans = numeric_limits<int>::max();

        // 1. 两次垂直切割
        for (int c1 = 0; c1 < C - 1; ++c1) {
            for (int c2 = c1 + 1; c2 < C - 1; ++c2) {
                int area1 = getArea(grid, 0, 0, R - 1, c1);
                int area2 = getArea(grid, 0, c1 + 1, R - 1, c2);
                int area3 = getArea(grid, 0, c2 + 1, R - 1, C - 1);
                if (area1 > 0 && area2 > 0 && area3 > 0) {
                    ans = min(ans, area1 + area2 + area3);
                }
            }
        }

        // 2. 两次水平切割
        for (int r1 = 0; r1 < R - 1; ++r1) {
            for (int r2 = r1 + 1; r2 < R - 1; ++r2) {
                int area1 = getArea(grid, 0, 0, r1, C - 1);
                int area2 = getArea(grid, r1 + 1, 0, r2, C - 1);
                int area3 = getArea(grid, r2 + 1, 0, R - 1, C - 1);
                if (area1 > 0 && area2 > 0 && area3 > 0) {
                    ans = min(ans, area1 + area2 + area3);
                }
            }
        }

        // 3. 第一次垂直切割，第二次水平切割 (增量优化)
        for (int c = 0; c < C - 1; ++c) {
            // 提取公共计算部分
            int area_right = getArea(grid, 0, c + 1, R - 1, C - 1);
            int area_left = getArea(grid, 0, 0, R-1, c);
            
            for (int r = 0; r < R - 1; ++r) {
                // 情况A: 左边部分被水平切割
                int area_left_up = getArea(grid, 0, 0, r, c);
                int area_left_down = getArea(grid, r + 1, 0, R - 1, c);
                if (area_left_up > 0 && area_left_down > 0 && area_right > 0) {
                    ans = min(ans, area_left_up + area_left_down + area_right);
                }
                
                // 情况B: 右边部分被水平切割
                int area_right_up = getArea(grid, 0, c + 1, r, C - 1);
                int area_right_down = getArea(grid, r + 1, c + 1, R - 1, C - 1);
                if (area_left > 0 && area_right_up > 0 && area_right_down > 0) {
                    ans = min(ans, area_left + area_right_up + area_right_down);
                }
            }
        }
        
        // 4. 第一次水平切割，第二次垂直切割 (增量优化)
        for (int r = 0; r < R - 1; ++r) {
            // 提取公共计算部分
            int area_down = getArea(grid, r + 1, 0, R - 1, C - 1);
            int area_up = getArea(grid, 0, 0, r, C-1);

            for (int c = 0; c < C - 1; ++c) {
                // 情况C: 上面部分被垂直切割
                int area_up_left = getArea(grid, 0, 0, r, c);
                int area_up_right = getArea(grid, 0, c + 1, r, C - 1);
                if (area_up_left > 0 && area_up_right > 0 && area_down > 0) {
                    ans = min(ans, area_up_left + area_up_right + area_down);
                }
                
                // 情况D: 下面部分被垂直切割
                int area_down_left = getArea(grid, r + 1, 0, R - 1, c);
                int area_down_right = getArea(grid, r + 1, c + 1, R - 1, C - 1);
                if (area_up > 0 && area_down_left > 0 && area_down_right > 0) {
                    ans = min(ans, area_up + area_down_left + area_down_right);
                }
            }
        }
        
        return ans;
    }
};

复杂度分析

代码主要由六个嵌套循环结构组成，每个结构都用于遍历一种特定的矩形切割方式。

getArea 辅助函数:
- 这个函数遍历一个由 (r1, c1) 和 (r2, c2) 确定的子网格。
- 它的时间复杂度是 O((r2 - r1 + 1) * (c2 - c1 + 1))，即子网格的大小。
- 在最坏情况下，它会遍历整个 grid，所以时间复杂度是 O(R * C)，其中 R 是行数，C 是列数。
主函数中的循环:
- 两次垂直切割: 两层嵌套循环，c1 从 0 到 C-2，c2 从 c1+1 到 C-2。这大约是 O(C^2) 次迭代。每次迭代内部调用三次 getArea。每次 getArea 的时间复杂度是 O(R * C)。因此，这部分的总时间复杂度是 O(C^2 * R * C) = O(R * C^3)。
- 两次水平切割: 类似地，两层嵌套循环，r1 和 r2 的范围是 O(R^2)。每次迭代调用三次 getArea。这部分的总时间复杂度是 O(R^2 * R * C) = O(R^3 * C)。
- 一次垂直一次水平切割（两种情况）:
  - 外层循环遍历垂直切割点 c，范围是 O(C)。
  - 内层循环遍历水平切割点 r，范围是 O(R)。
  - 每次内层循环都调用三次 getArea，每次调用的时间复杂度是 O(R * C)。
  - 这部分的总时间复杂度是 O(C * R * R * C) = O(R^2 * C^2)。由于有两种类似的情况，总的复杂度仍然是 O(R^2 * C^2)。
- 一次水平一次垂直切割（两种情况）:
  - 与上面类似，外层循环 r 的范围是 O(R)，内层循环 c 的范围是 O(C)。
  - 每次内层循环调用三次 getArea，每次 O(R * C)。
  - 总时间复杂度是 O(R * C * R * C) = O(R^2 * C^2)。

结论

综上所述，整个算法的时间复杂度由最高阶项决定。

$O(R⋅C^3)$
$O(R^3⋅C)$
$O(R^2⋅C^2)$

由于题目中 R 和 C 的最大值都是 30，可以认为它们在同一量级。所以，总的时间复杂度可以概括为 $O(N^4)$，其中 N 是网格的边长（约 30）。

3197. 包含所有 1 的最小矩形面积 II

beautifulremi

题目

解题思路

代码实现

优化思路

优化后代码

复杂度分析

结论