题目

给你一个二维 二进制 数组 grid。请你找出一个边在水平方向和竖直方向上、面积最小的矩形，并且满足 grid 中所有的 1 都在矩形的内部。

返回这个矩形可能的最小面积。

示例 1：

输入： grid = [[0,1,0],[1,0,1]]

输出： 6

解释：

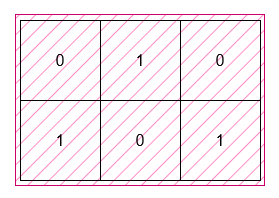
这个最小矩形的高度为 2，宽度为 3，因此面积为 2 * 3 = 6。

示例 2：

输入： grid = [[0,0],[1,0]]

输出： 1

解释：

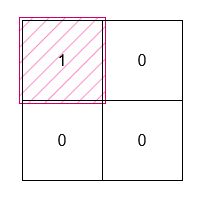
这个最小矩形的高度和宽度都是 1，因此面积为 1 * 1 = 1。

提示：

1 <= grid.length, grid[i].length <= 1000
grid[i][j] 是 0 或 1。
输入保证 grid 中至少有一个 1 。

解题思路

为了让包含所有 1 的矩形面积最小，这个矩形的四条边必须 "紧贴" 着最外围的 1。

具体来说，这个矩形的：

上边界 应该由最靠上的 1 所在的行决定。
下边界 应该由最靠下的 1 所在的行决定。
左边界 应该由最靠左的 1 所在的列决定。
右边界 应该由最靠右的 1 所在的列决定。

所以，问题就转化为了：遍历整个二维数组，找出所有 1 中，最小的行号、最大的行号、最小的列号和最大的列号。

解题步骤

初始化边界变量：
- min_row (最小行号)：可以初始化为一个非常大的数（例如，grid 的行数，或者 Infinity）。
- max_row (最大行号)：可以初始化为一个非常小的数（例如，-1）。
- min_col (最小列号)：可以初始化为一个非常大的数（例如，grid 的列数，或者 Infinity）。
- max_col (最大列号)：可以初始化为一个非常小的数（例如，-1）。
遍历数组：
- 使用嵌套循环遍历 grid 中的每一个元素 grid[i][j]（其中 i 是行号，j 是列号）。
- 当遇到一个 1 (grid[i][j] == 1) 时，就用当前的行号 i 和列号 j 来更新我们的四个边界变量：
  - min_row = min(min_row, i)
  - max_row = max(max_row, i)
  - min_col = min(min_col, j)
  - max_col = max(max_col, j)
计算面积：
- 遍历结束后，我们就得到了包裹所有 1 的最小矩形的四个边界。
- 矩形的高度为：height = max_row - min_row + 1。
- 矩形的宽度为：width = max_col - min_col + 1。
- 最终的最小面积就是 area = height * width。

代码实现

class Solution {
public:
    int minimumArea(vector<vector<int>>& grid) {
        
        int m = grid.size();
        int n = grid[0].size();
        int top = m;
        int bottom = -1;
        int left = n;
        int right = -1;

        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                if(grid[i][j] == 1)
                {
                    top = std::min(top, i);
                    bottom = std::max(bottom, i);
                    left = std::min(left, j);
                    right = std::max(right, j);
                }
            }
        }
        
        int height = bottom - top + 1;
        int width = right - left + 1;
        
        return width * height;
    }
};

3195. 包含所有 1 的最小矩形面积 I

beautifulremi

题目

解题思路

解题步骤

代码实现