题目

给你两个整数 numBottles 和 numExchange 。

numBottles 代表你最初拥有的满水瓶数量。在一次操作中，你可以执行以下操作之一：

喝掉任意数量的满水瓶，使它们变成空水瓶。
用 numExchange 个空水瓶交换一个满水瓶。然后，将 numExchange 的值增加 1 。

注意，你不能使用相同的 numExchange 值交换多批空水瓶。例如，如果 numBottles == 3 并且 numExchange == 1 ，则不能用 3 个空水瓶交换成 3 个满水瓶。

返回你最多可以喝到多少瓶水。

示例 1：

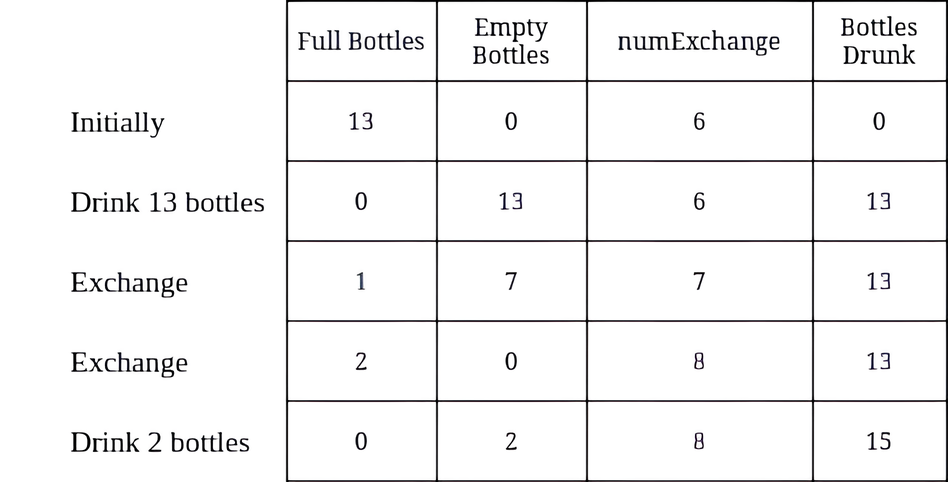
输入：numBottles = 13, numExchange = 6 输出：15 解释：上表显示了满水瓶的数量、空水瓶的数量、numExchange 的值，以及累计喝掉的水瓶数量。

示例 2：

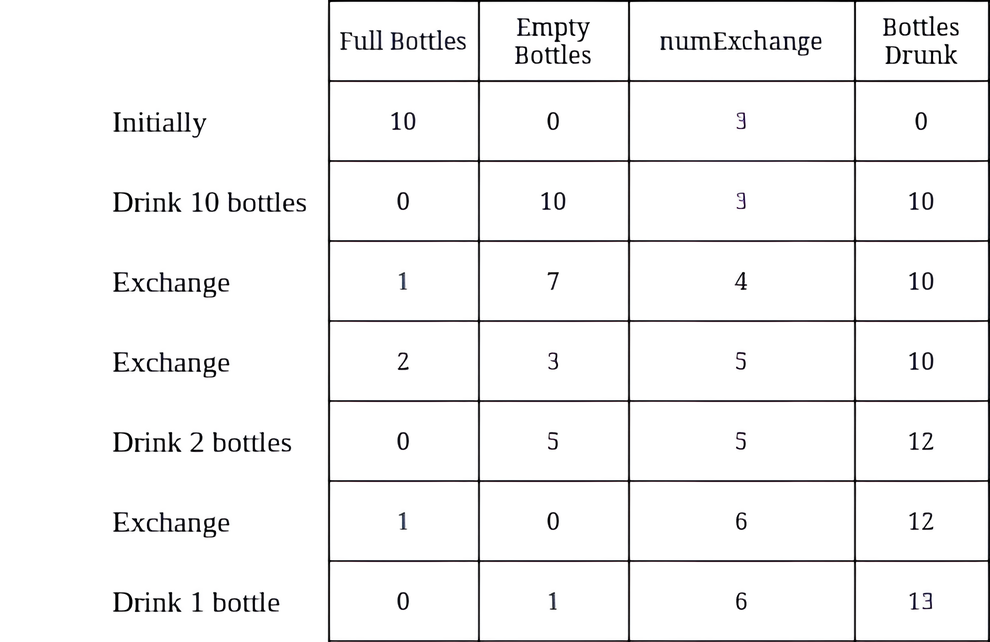
输入：numBottles = 10, numExchange = 3 输出：13 解释：上表显示了满水瓶的数量、空水瓶的数量、numExchange 的值，以及累计喝掉的水瓶数量。

提示：

1 <= numBottles <= 100
1 <= numExchange <= 100

解题思路

模拟法

初始化状态：
- 你最开始拥有 numBottles 瓶满水瓶。
- 一个显而易见的最佳策略是：先把手头所有的满水瓶都喝掉。
- 所以，你喝掉的总数（totalDrunk）初始化为 numBottles。
- 喝完后，这些瓶子都变成了空瓶，所以你拥有的空瓶数（emptyBottles）也初始化为 numBottles。
- 兑换所需的瓶子数 numExchange 保持不变。
循环兑换和喝水：
- 接下来，进入一个循环。循环的条件是：你拥有的空瓶数量是否足够进行下一次兑换？ 也就是 emptyBottles >= numExchange。
- 只要这个条件成立，你就应该执行一次兑换操作，因为这样能喝到更多的水。
在循环内部，模拟一次完整的“兑换-喝水”流程：
- 兑换：你用 numExchange 个空瓶换了 1 瓶满水。
  - 你的空瓶数减少了 numExchange 个。 (emptyBottles = emptyBottles - numExchange)
- 喝水：你立即把这 1 瓶新换来的水喝掉。
  - 你喝掉的总数增加了 1。 (totalDrunk = totalDrunk + 1)
  - 这瓶刚喝完的水又变成了一个新的空瓶，所以你的空瓶数增加了 1。 (emptyBottles = emptyBottles + 1)
- 更新兑换条件：根据题目要求，在完成这次兑换后，下一次兑换所需的空瓶数会增加 1。
  - 所以，你需要更新 numExchange 的值。 (numExchange = numExchange + 1)
结束循环：
- 当循环条件 emptyBottles >= numExchange 不再满足时，意味着你手上的空瓶已经不足以进行任何新的兑换了。
- 此时，模拟过程结束。变量 totalDrunk 中记录的数值就是你最多能喝到的水瓶数量。

数学公式法

当你用 k 个空瓶兑换 1 瓶水时，你并不是永久失去了 k 个瓶子。因为喝完后，这 1 瓶水会变回 1 个空瓶。
因此，每完成一次兑换，你实际永久性失去或净消耗的空瓶数量是 k - 1 个。
你最初拥有的 numBottles 个瓶子就是你的全部“资本”，所有的“净消耗”都必须从这个资本里出。

下一步是建立一个公式，来计算完成 n 次兑换所需的总净消耗。

第 1 次兑换，净消耗：(numExchange + 0) - 1
第 2 次兑换，净消耗：(numExchange + 1) - 1
第 3 次兑换，净消耗：(numExchange + 2) - 1
...
第 n 次兑换，净消耗：(numExchange + n - 1) - 1

将这 n 次的净消耗全部相加，通过等差数列求和，得到总净消耗公式 TotalNetCost(n): $$TotalNetCost(n)=n\cdot(numExchange-1)+\frac{n(n-1)}{2}$$ 现在问题转化为：在“资本”的限制下，求解 n 的最大值。

资本限制：你最多能承受的净消耗就是你最初的瓶子数。在你的代码实现中，这个限制被精确地定义为 numBottles - 1（因为总需要有瓶子在系统中流转）。
求解目标：找到一个最大的整数 $n_{max}$，使其满足以下不等式： $$TotalNetCost(n_{max})\leq numBottles-1$$ 这个求解过程可以通过循环迭代来实现：从 n=1 开始，不断计算 TotalNetCost(n)，直到它超出 numBottles - 1 为止。

一旦找到了最大可兑换次数 nmax，最终结果就很容易计算了。

你最初喝了 numBottles 瓶。
通过兑换，你额外喝了 $n_{max}$ 瓶。
所以，你总共能喝到的水瓶数量为： $$\text{总数}=numBottles+n_{max}$$

具体代码

模拟法

func maxBottlesDrunk(numBottles int, numExchange int) int {

	// --- 步骤 1: 初始化状态 ---

	// 首先，将初始拥有的水瓶全部喝掉。
	// totalDrunk 用于累计总共喝掉的水瓶数量。
	var totalDrunk = numBottles

	// 喝完后，这些满水瓶全部变成了空瓶。
	// emptyBottles 用于追踪当前持有的空瓶数量。
	var emptyBottles = numBottles

	// --- 步骤 2: 进入循环，模拟兑换过程 ---

	// 循环条件：只要我们拥有的空瓶数量，足够支付下一次兑换的成本，就继续。
	for emptyBottles >= numExchange {
		
		// --- 在循环内部，执行一次完整的“兑换-喝水”流程 ---

		// a) 支付兑换成本：用持有的空瓶进行兑换。
		emptyBottles -= numExchange

		// b) 获得新水瓶并喝掉：总共喝掉的数量加 1。
		totalDrunk++

		// c) 新瓶变空瓶：刚喝完的这瓶水，也变成了一个空瓶，加入我们的空瓶库存。
		emptyBottles++

		// d) 更新兑换成本：根据规则，下一次兑换会变得更“贵”。
		numExchange++
	}

	// --- 步骤 3: 返回最终结果 ---

	// 当循环结束时，意味着剩余的空瓶已经不足以进行任何新的兑换。
	// 此时 totalDrunk 中累计的数量就是最终的答案。
	return totalDrunk
}

数学公式法

func maxBottlesDrunk(numBottles int, numExchange int) int {

	
	// successfulExchanges 用于记录我们最终能成功完成的兑换次数。
	var successfulExchanges int = 0

	// 我们使用一个无限循环来逐一尝试可以兑换多少次。
	// attemptedExchanges 代表我们“正在尝试”的兑换次数，从1开始。
	for attemptedExchanges := 1; ; attemptedExchanges++ {
		
		// 步骤 1: 计算尝试进行 `attemptedExchanges` 次兑换所需的总净消耗。
		netCost := attemptedExchanges*(numExchange-1) + (attemptedExchanges*(attemptedExchanges-1))/2

		// 步骤 2: 判断我们的“资本”是否足够支付这次尝试。
		// 可消耗的资本上限是 numBottles - 1。
		if netCost > numBottles-1 {
			// 如果 `netCost` 超出了我们的承受能力，
			// 意味着我们无法完成 `attemptedExchanges` 次兑换。
			// 那么，我们能成功完成的最大次数就是上一次的尝试，即 `attemptedExchanges - 1`。
			successfulExchanges = attemptedExchanges - 1
			
			// 既然已经找到了最大次数，就立即跳出循环。
			break
		}
	}

	// 步骤 3: 计算最终结果。
	// 总共喝的数量 = 初始数量 + 成功兑换的次数。
	return numBottles + successfulExchanges
}

3100. 换水问题 II

beautifulremi

题目

解题思路

模拟法

数学公式法

具体代码

模拟法

数学公式法