题目

给你一个 n x 2 的二维数组 points ，它表示二维平面上的一些点坐标，其中 points[i] = [xi, yi] 。

计算点对 (A, B) 的数量，其中

A 在 B 的左上角，并且
它们形成的长方形中（或直线上）没有其它点（包括边界）。

返回数量。

示例 1：

输入：points = [[1,1],[2,2],[3,3]]

输出：0

解释：

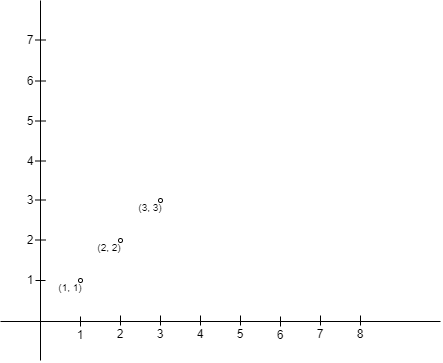
没有办法选择 A 和 B，使得 A 在 B 的左上角。

示例 2：

输入：points = [[6,2],[4,4],[2,6]]

输出：2

解释：

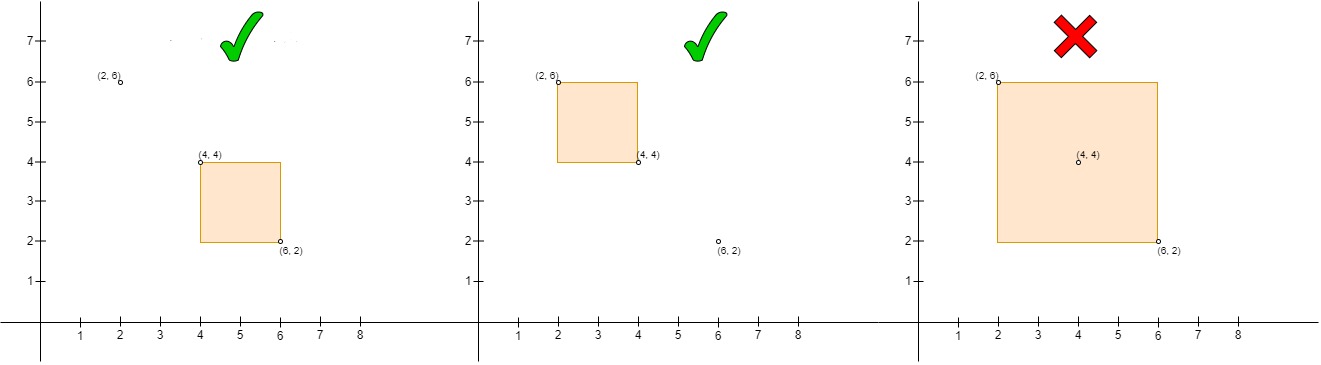
左边的是点对 (points[1], points[0])，其中 points[1] 在 points[0] 的左上角，并且形成的长方形内部是空的。
中间的是点对 (points[2], points[1])，和左边的一样是合法的点对。
右边的是点对 (points[2], points[0])，其中 points[2] 在 points[0] 的左上角，但 points[1] 在长方形内部，所以不是一个合法的点对。

示例 3：

输入：points = [[3,1],[1,3],[1,1]]

输出：2

解释：

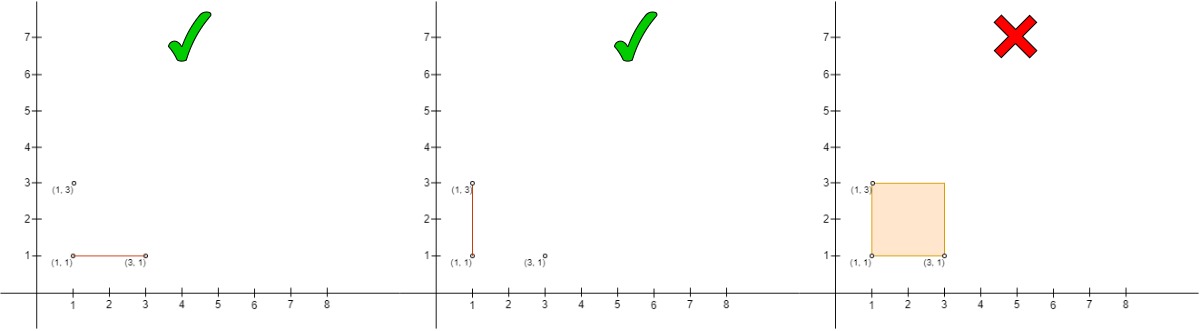
左边的是点对 (points[2], points[0])，其中 points[2] 在 points[0] 的左上角并且在它们形成的直线上没有其它点。注意两个点形成一条线的情况是合法的。
中间的是点对 (points[1], points[2])，和左边一样也是合法的点对。
右边的是点对 (points[1], points[0])，它不是合法的点对，因为 points[2] 在长方形的边上。

提示：

2 <= n <= 50
points[i].length == 2
0 <= points[i][0], points[i][1] <= 50
points[i] 点对两两不同。

解题思路

建立有序性（预处理）：首先，为了避免毫无章法地随意检查点对，第一步是对所有的点进行一次有目的的排序。一个有效的策略是从左到右，从上到下地对所有点进行排列。这一步的目的是为后续的检查建立一个清晰、有序的框架，使得我们能够系统性地、不重复、不遗漏地考察所有可能的点对。
系统性地枚举和筛选候选点对：在排好序的基础上，我们开始系统地寻找可能的点对 (A, B)。具体做法是，我们依次固定每一个点作为潜在的右下角点 B。然后，对于每一个固定的 B，我们回头去看所有在它“前面”（根据我们第一步的排序规则）的点，将它们作为潜在的左上角点 A。通过这种方式，我们只考虑那些在位置上可能构成“左上-右下”关系的点对，排除了大量明显不符的组合。
验证“空矩形”区域：对于每一个经过上一步筛选出的候选点对 (A, B)，我们执行最后也是最关键的验证。我们以 A 和 B 为对角顶点，构想一个矩形。然后，我们检查除了 A 和 B 以外，是否存在任何其他的点落在了这个矩形的内部或边界上。
- 如果存在任何一个这样的“第三者”点，那么这个点对 (A, B) 就是无效的。
- 只有当这个矩形区域内是“空的”，这个点对 (A, B) 才是一个符合题目要求的合法点对，我们就把它计数下来。

具体代码

class Solution {
public:
    int numberOfPairs(vector<vector<int>>& points) {

        //  自上而下，自左而右排序
        sort(points.begin(), points.end(),
        [](const vector<int>& a, const vector<int>& b)
        {
            return a[0] < b[0] || (a[0] == b[0] && a[1] > b[1]);
        });

        int n = points.size();
        bool currentPass = true;
        int ans = 0;
        for(int i = 0; i < n; i++) // 选定每个右下角的点
        {
            for(int j = 0; j < i; j++) // 选定理论上每个左上角的点
            {
                // 检验是不是左上角的点
                if(!(points[j][0] <= points[i][0] && points[j][1] >= points[i][1]))
                    continue;

                currentPass = true;

                for(int k = j + 1; k < i; k++) // 检验可能在内部的点
                {
                    if(points[k][0] >= points[j][0] && points[k][0] <= points[i][0] && points[k][1] >= points[i][1] && points[k][1] <= points[j][1]) // 检验内部点
                    {
                        currentPass = false; // 不合法点对
                        break;
                    }

                }
                // 合法点对
                if(currentPass)
                    ans++;
            }
        }

        return ans;
        
    }
};

优化思路

固定右下角点 B，然后寻找所有可能的左上角点 A，再用第三层循环去检查 A 和 B 之间是否有障碍点。这个检查过程是导致 O(N³) 的主要原因。

我们可以转换一下视角：固定左上角点 A，然后向右寻找所有可能的右下角点 B。

具体思路如下：

保持排序不变：排序方法（x 坐标升序，x 相同则 y 坐标降序）不变，这个优化思路依然依赖于它。
转换主视角：我们写一个外层循环，固定点 A (points[j])。然后内层循环向右遍历 (i 从 j+1 到 n-1)，寻找所有可以与 A 配对的点 B (points[i])。
核心优化：维护一个“下边界” 对于一个固定的 A，当我们向右寻找 B 时，一个点 B 要能和 A 配对，必须满足两个条件： a. B 在 A 的右下方（B.y <= A.y）。 b. A 和 B 构成的矩形区域内没有其他点。这里的关键是条件 b。当我们在 j 的右侧遍历 i 时，所有考察过的点 points[k] (j < k < i) 都是潜在的“障碍物”。一个点 points[k] 会阻碍 (A, B) 配对，当且仅当它位于矩形内部，即 B.y <= points[k].y <= A.y。为了避免每次都循环检查这些障碍物，我们可以为固定的 A 维护一个变量，称之为 y_lower_bound（下边界）。这个变量记录了在 A 和当前考察点 B 之间、且在 A 下方的所有点中，y 坐标的最大值。
- 当我们考察一个新的点 B (points[i]) 时，如果 B.y <= A.y，它就是一个候选点。
- 这时，我们检查它是否满足 B.y > y_lower_bound。
  - 如果满足，说明在 A 和 B 之间没有任何点的 y 坐标落入 [B.y, A.y] 的区间内。因此，(A, B) 构成一个合法的点对，我们计数加一。同时，因为 B 本身也可能成为后续点对的障碍，我们需要更新 y_lower_bound = max(y_lower_bound, B.y)。
  - 如果不满足，说明 B 点被 y_lower_bound 代表的那个“最高”的障碍物挡住了，(A, B) 不是合法点对。但我们仍然需要更新 y_lower_bound，因为它下面的空间已经被填充了。

通过这种方式，对于每一个固定的 A，我们只需要一层循环向右扫描，并在 O(1) 的时间内完成判断，从而将总时间复杂度降至 O(N²)。

优化代码

class Solution {
public:
    int numberOfPairs(vector<vector<int>>& points) {
        // 排序规则：x 坐标升序，x 相同则 y 坐标降序
        sort(points.begin(), points.end(),
        [](const vector<int>& a, const vector<int>& b)
        {
            return a[0] < b[0] || (a[0] == b[0] && a[1] > b[1]);
        });

        int n = points.size();
        int ans = 0;

        // O(N^2) 解法
        // 外层循环固定左上角点 A (points[j])
        for (int j = 0; j < n; ++j) {
            // y_lower_bound 记录了在 A 和 B 之间、且在 A 下方的所有点中，y坐标的最大值。
            // 初始为一个极小值。
            int y_lower_bound = numeric_limits<int>::min();

            // 内层循环从 A 的右侧开始，寻找所有可能的右下角点 B (points[i])
            for (int i = j + 1; i < n; ++i) {
                
                // 当前点 B 的 y 坐标
                int current_y = points[i][1];

                // A 点的 y 坐标
                int upper_y = points[j][1];

                // B 必须在 A 的下方或同一水平线 (current_y <= upper_y)
                // 并且 B 必须在 "下边界" 上方 (current_y > y_lower_bound)
                // 这同时满足了两个条件：
                // 1. B 是 A 的右下角点
                // 2. 在 A 和 B 之间，不存在任何点 p_k 使得 B.y <= p_k.y <= A.y
                if (current_y <= upper_y && current_y > y_lower_bound) {
                    ans++;
                    // 找到一个合法的 B 之后，它就会成为新的“下边界”，
                    // 因为任何在它右边且比它更低的点都会被它遮挡。
                    y_lower_bound = current_y;
                }
            }
        }

        return ans;
    }
};

3025. 人员站位的方案数 I

beautifulremi

题目

解题思路

具体代码

优化思路

优化代码