题目

给你一棵 n 个节点的无向树，节点编号为 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 有一条边。

同时给你一个下标从 0 开始长度为 n 的整数数组 values ，其中 values[i] 是第 i 个节点的值。再给你一个整数 k 。

你可以从树中删除一些边，也可以一条边也不删，得到若干连通块。一个 连通块的值 定义为连通块中所有节点值之和。如果所有连通块的值都可以被 k 整除，那么我们说这是一个 合法分割 。

请你返回所有合法分割中，连通块数目的最大值 。

示例 1：

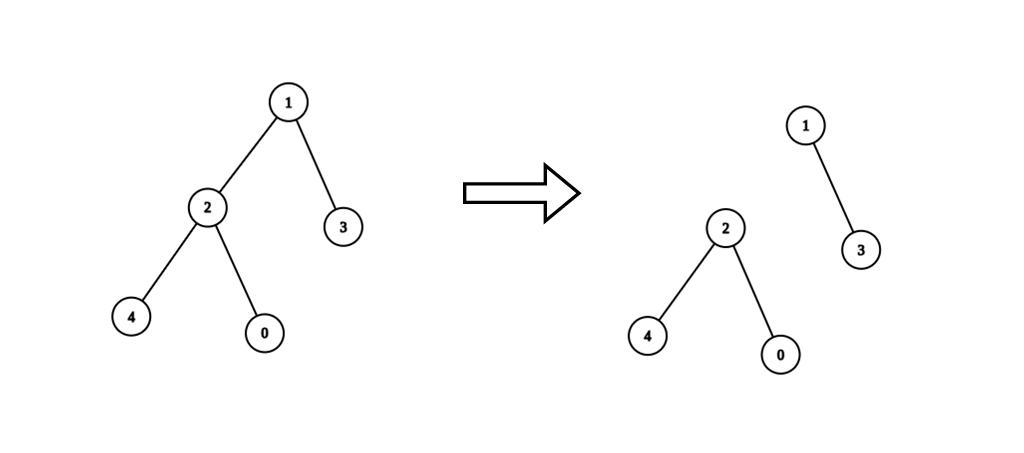
输入：n = 5, edges = [[0,2],[1,2],[1,3],[2,4]], values = [1,8,1,4,4], k = 6 输出：2 解释：我们删除节点 1 和 2 之间的边。这是一个合法分割，因为：

节点 1 和 3 所在连通块的值为 values[1] + values[3] = 12 。
节点 0 ，2 和 4 所在连通块的值为 values[0] + values[2] + values[4] = 6 。最多可以得到 2 个连通块的合法分割。

示例 2：

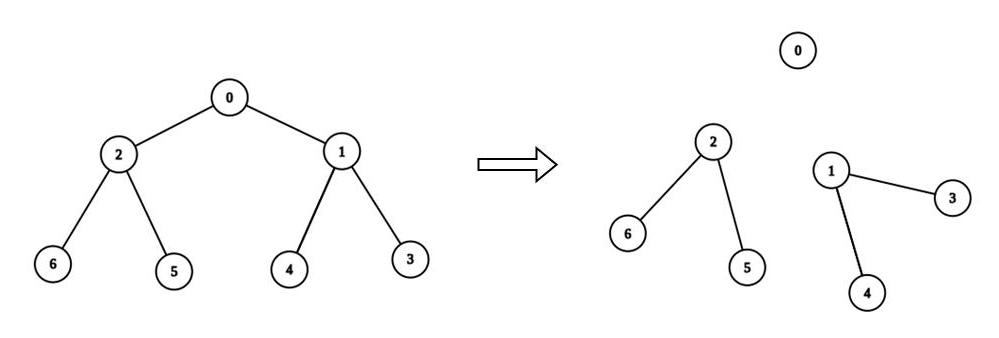
输入：n = 7, edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], values = [3,0,6,1,5,2,1], k = 3 输出：3 解释：我们删除节点 0 和 2 ，以及节点 0 和 1 之间的边。这是一个合法分割，因为：

节点 0 的连通块的值为 values[0] = 3 。
节点 2 ，5 和 6 所在连通块的值为 values[2] + values[5] + values[6] = 9 。
节点 1 ，3 和 4 的连通块的值为 values[1] + values[3] + values[4] = 6 。最多可以得到 3 个连通块的合法分割。

提示：

1 <= n <= 3 * 10^4
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
values.length == n
0 <= values[i] <= 10^9
1 <= k <= 10^9
values 之和可以被 k 整除。
输入保证 edges 是一棵无向树。

解题思路

题目的目标是让连通块的数量最大化。我们可以从树的叶子节点向上思考：

对于任意一个以节点 u 为根的子树，计算该子树中所有节点的权值之和 sum_u。
如果 sum_u 能够被 k 整除（即 sum_u % k == 0）：
- 这说明这颗子树本身就可以形成一个合法的连通块。
- 为了让连通块数量最大，我们应该贪心地把这颗子树从父节点处“切断”。
- 切断后，这颗子树贡献了 1 个连通块，且它对父节点所在的剩余部分的“余数贡献”变为 0（因为它已经被整除拿走了）。
如果 sum_u 不能被 k 整除：
- 这颗子树不能单独切断，它必须依附于父节点，希望能和父节点以及其他兄弟节点凑出一个能被 k 整除的总和。
- 它对父节点的贡献就是 sum_u 的值（或者说 sum_u % k）。

结论：我们在进行深度优先搜索（DFS）时，每当发现一个子树的权值和能被 k 整除，我们就把连通块计数器 +1，并认为该子树对上层的贡献为 0（相当于切断了）。

详细算法步骤

建图：利用题目给出的 edges 数组，构建邻接表（Adjacency List），方便进行树的遍历。
DFS 遍历（后序遍历）：从任意节点（比如节点 0）开始进行 DFS。DFS 函数的作用是返回当前子树剩余的、未能被 k 整除的权值和。
递归逻辑：对于当前节点 u：
- 初始化 current_sum = values[u]。
- 遍历 u 的所有邻居节点 v（跳过父节点 parent，防止死循环）。
- 递归调用 DFS(v)，将返回值加到 current_sum 上。
- 检查判断：
  - 如果 current_sum % k == 0：说明以 u 为根（包含其未切断的子孙）形成的连通块是合法的。我们将全局计数器 count 加 1，并返回 0 给上层（表示这部分切掉了，不给上面留负担）。
  - 如果 current_sum % k != 0：说明当前部分还凑不够 k 的倍数，必须连着父节点。返回 current_sum 给上层。
返回结果： DFS 结束后，count 即为最大连通块数量。注意：题目保证了整个树的总和能被 k 整除，所以根节点的 DFS 最后一次判断一定会让 count + 1。

具体代码

func maxKDivisibleComponents(n int, edges [][]int, values []int, k int) int {
    // 1. 构建邻接表
    // adj[i] 存储节点 i 的所有邻居
    adj := make([][]int, n)
    for _, e := range edges {
        u, v := e[0], e[1]
        adj[u] = append(adj[u], v)
        adj[v] = append(adj[v], u)
    }

    ans := 0

    // 2. 定义 DFS 函数
    // 返回值：当前子树中，除去已形成合法连通块的部分外，剩余的权值之和
    var dfs func(u, p int) int
    dfs = func(u, p int) int {
        // 初始化当前子树和为节点自身的值
        sum := values[u]

        // 遍历邻居
        for _, v := range adj[u] {
            if v == p {
                continue // 跳过父节点，防止死循环
            }
            // 累加子节点的剩余贡献
            sum += dfs(v, u)
        }

        // 3. 贪心策略
        // 如果当前子树的总和能被 k 整除
        if sum % k == 0 {
            ans++    // 记录为一个合法的连通块
            return 0 // 该子树已“独立”，对父节点不再有数值贡献
        }

        // 否则，返回当前和，继续向上合并
        return sum
    }

    // 从根节点 0 开始，父节点设为 -1
    dfs(0, -1)

    return ans
}

2872. 可以被 K 整除连通块的最大数目

beautifulremi

题目

解题思路

详细算法步骤

具体代码