题目

给你一个下标从 0 开始的 m x n 整数矩阵 grid 和一个整数 k 。你从起点 (0, 0) 出发，每一步只能往下或者往右，你想要到达终点 (m - 1, n - 1) 。

请你返回路径和能被 k 整除的路径数目，由于答案可能很大，返回答案对 109 + 7 取余的结果。

示例 1：

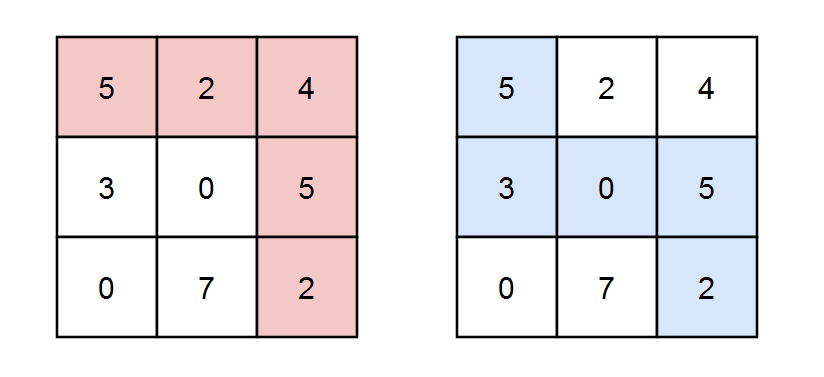
输入：grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3 输出：2 解释：有两条路径满足路径上元素的和能被 k 整除。第一条路径为上图中用红色标注的路径，和为 5 + 2 + 4 + 5 + 2 = 18 ，能被 3 整除。第二条路径为上图中用蓝色标注的路径，和为 5 + 3 + 0 + 5 + 2 = 15 ，能被 3 整除。

示例 2：

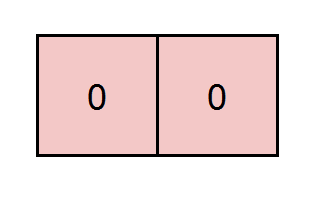
输入：grid = [[0,0]], k = 5 输出：1 解释：红色标注的路径和为 0 + 0 = 0 ，能被 5 整除。

示例 3：

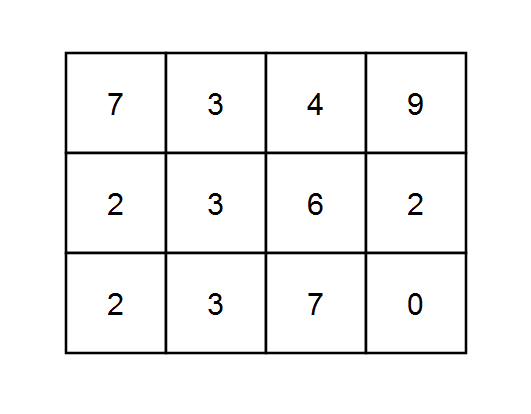
输入：grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1 输出：10 解释：每个数字都能被 1 整除，所以每一条路径的和都能被 k 整除。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 5 * 10^4
1 <= m * n <= 5 * 10^4
0 <= grid[i][j] <= 100
1 <= k <= 50

解题思路

这道题是一道典型的 动态规划 (Dynamic Programming) 结合 模运算 的题目。

1. 核心思路分析

我们需要找到从 (0, 0) 到 (m-1, n-1) 的路径，使得路径和能被 k 整除。

如果我们直接记录路径的和，数值会非常大，无法作为 DP 的状态。但是，题目只关心“能否被 k 整除”，根据模运算的性质：$(A + B) \mod k = ((A \mod k) + (B \mod k)) \mod k$。

这意味着我们不需要记录具体的“和”，只需要记录路径和 对 k 取模后的余数。

2. 动态规划设计

(1) 定义状态

定义 dp[i][j][r] 为：

从起点 (0, 0) 到达网格位置 (i, j) 时，路径和除以 k 的余数为 r 的路径数量。

i: 行索引，$0 \le i < m$
j: 列索引，$0 \le j < n$
r: 余数，$0 \le r < k$

(2) 状态转移方程

对于位置 (i, j)，它只能从上方 (i-1, j) 或左方 (i, j-1) 移动过来。

假设当前格子的数值为 grid[i][j]，如果我们希望到达 (i, j) 后的总和余数是 r，那么前一步的余数 prev_r 必须满足：

$$(prev_r + grid[i][j]) % k = r$$

反推 prev_r：

$$prev_r = (r - grid[i][j]) % k$$

(注意：在某些编程语言如 C++/Java 中，负数取模需要特殊处理，写成 (r - grid[i][j] % k + k) % k)

因此，转移方程为：

$$dp[i][j][r] = dp[i-1][j][prev_r] + dp[i][j-1][prev_r]$$

(记得对 $10^9 + 7$ 取模)

(3) 初始化（Base Case）

起点 (0, 0) 的数值是 grid[0][0]。

所以在位置 (0, 0)，只有一种余数是可能的，即 grid[0][0] % k。

dp[0][0][grid[0][0] % k] = 1
dp[0][0][其他余数] = 0

(4) 最终答案

我们需要的是到达终点 (m-1, n-1) 且路径和能被 k 整除（余数为 0）的路径数。

答案即为：dp[m-1][n-1][0]。

3. 复杂度分析

时间复杂度：$O(m \times n \times k)$
- 我们需要遍历网格的每个位置 $(m \times n)$。
- 对于每个位置，我们需要计算 $k$ 个余数状态。
- 题目中 $m \times n \le 5 \times 10^4$，$k \le 50$，总计算量约为 $2.5 \times 10^6$，远小于一般的时间限制（$10^8$），所以非常安全。
空间复杂度：$O(m \times n \times k)$
- 需要存储三维数组。
- 可以优化为 $O(n \times k)$，因为计算第 i 行只需要第 i-1 行的数据（滚动数组优化）。

具体代码

func numberOfPaths(grid [][]int, k int) int {

    // 初始化
    const REMAIN = 1000000007
    m := len(grid)
    n := len(grid[0])
    dp := make([][][]int, m)
    for i := range dp {
        dp[i] = make([][]int, n)
        for j := range dp[i] {
            dp[i][j] = make([]int, k)
        }
    }
    dp[0][0][grid[0][0] % k] = 1

    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            for l := 0; l < k; l++ {
                if dp[i][j][l] != 0 {

                    if i + 1 < m {
                        dp[i + 1][j][(l + grid[i + 1][j]) % k] = (dp[i][j][l] + dp[i + 1][j][(l + grid[i + 1][j]) % k]) % REMAIN
                    }
                    
                    if j + 1 < n {
                        dp[i][j + 1][(l + grid[i][j + 1]) % k] = (dp[i][j][l] + dp[i][j + 1][(l + grid[i][j + 1]) % k]) % REMAIN
                    }
                    
                }
            }
        }
    }

    return dp[m - 1][n - 1][0]
}

2435. 矩阵中和能被 K 整除的路径

beautifulremi

题目