题目

存在一棵无向连通树，树中有编号从 0 到 n - 1 的 n 个节点， 以及 n - 1 条边。

给你一个下标从 0 开始的整数数组 nums ，长度为 n ，其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。

删除树中两条 不同 的边以形成三个连通组件。对于一种删除边方案，定义如下步骤以计算其分数：

1. 分别获取三个组件 每个 组件中所有节点值的异或值。
2. 最大 异或值和 最小 异或值的 差值 就是这一种删除边方案的分数。

• 例如，三个组件的节点值分别是：[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = 6、1 ^ 9 = 8 和 3 ^ 3 ^ 3 = 3 。最大异或值是 8 ，最小异或值是 3 ，分数是 8 - 3 = 5 。

返回在给定树上执行任意删除边方案可能的 最小 分数。

示例 1：

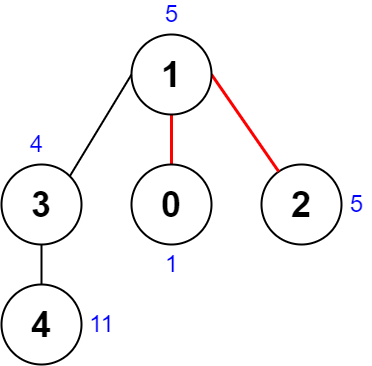
输入：nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]] 输出：9 解释：上图展示了一种删除边方案。

• 第 1 个组件的节点是 [1,3,4] ，值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。
• 第 2 个组件的节点是 [0] ，值是 [1] 。异或值是 1 = 1 。
• 第 3 个组件的节点是 [2] ，值是 [5] 。异或值是 5 = 5 。 分数是最大异或值和最小异或值的差值，10 - 1 = 9 。 可以证明不存在分数比 9 小的删除边方案。

示例 2：

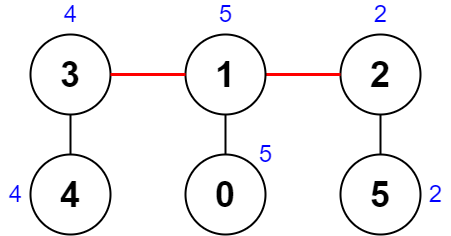
输入：nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]] 输出：0 解释：上图展示了一种删除边方案。

• 第 1 个组件的节点是 [3,4] ，值是 [4,4] 。异或值是 4 ^ 4 = 0 。
• 第 2 个组件的节点是 [1,0] ，值是 [5,5] 。异或值是 5 ^ 5 = 0 。
• 第 3 个组件的节点是 [2,5] ，值是 [2,2] 。异或值是 2 ^ 2 = 0 。 分数是最大异或值和最小异或值的差值，0 - 0 = 0 。 无法获得比 0 更小的分数 0 。

提示：

• n == nums.length
• 3 <= n <= 1000
• 1 <= nums[i] <= 10^8
• edges.length == n - 1
• edges[i].length == 2
• 0 <= a_i, b_i < n
• a_i != b_i
• edges 表示一棵有效的树

解题思路

题意分析

• 输入：一棵有 n 个节点的树，每个节点有权值 nums[i]。
• 操作：删除两条不同的边。
• 结果：树被分成三个独立的连通组件。
• 计分：计算每个组件内所有节点权值的异或和，得到三个值 x1, x2, x3。该方案的得分为 max(x1, x2, x3) - min(x1, x2, x3)。
• 目标：找到所有删除方案中，可能的最小得分。

异或的性质

异或运算有一个非常重要的性质：a ^ a = 0，以及 a ^ b ^ b = a。 如果我们知道整棵树所有节点值的异或和 total_xor，以及三个组件的异或和 x1, x2, x3，那么必然满足：

x1​⊕x2​⊕x3​=total_xor

(这里 ⊕ 表示异或)

这意味着，只要我们确定了其中两个组件的异或和（比如 x1 和 x2），第三个组件的异或和 x3 也就随之确定了：

x3​=total_xor⊕x1​⊕x2​

因此，问题转化成了：如何找到所有可能的 x1 和 x2 的组合，并计算对应的 x3，从而找出最小的分数。

切割子树

在树中，每删除一条边 (u, v)，都会将树分成两个组件。如果我们把树看作是以某个节点（比如 0）为根的有根树，那么删除边 (parent, child)，实际上就是将以 child 为根的整个子树分离出去。

• 组件1：以 child 为根的子树。
• 组件2：树的其余部分。

这个子树的节点值异或和，可以通过一次深度优先搜索（DFS），采用后序遍历的方式高效地计算出来。

解题步骤

步骤一：预处理 - 计算所有子树的异或和

1. 构建邻接表：根据输入的 edges 数组，构建一个图的邻接表，方便进行遍历。
2. 计算总异或和：遍历 nums 数组，计算出整棵树所有节点值的异或和 total_xor。
3. 执行 DFS：我们还会需要判断两个子树的拓扑关系（一个是否包含另一个）。这也可以在 DFS 中通过记录每个节点的父节点或者子树的节点范围来实现。
   • 从根节点（例如节点 0）开始进行深度优先搜索。
   • DFS 函数 dfs(u, parent) 的作用是计算并返回以节点 u 为根的子树中所有节点值的异或和。
   • 在 DFS 的后序遍历位置（即访问完 u 的所有子节点之后），计算 u 的子树异或和：xor_sum[u] = nums[u] ^ xor_sum[child1] ^ xor_sum[child2] ^ ...。
   • 将每个节点 u（除了根节点）对应的子树异或和 xor_sum[u] 记录下来。这些值就是我们通过切一刀能得到的所有可能的组件异或和。

步骤二：遍历所有切割方案并计算分数

现在我们有了所有单次切割能产生的子树异或和。我们需要模拟切割两次。假设我们切割两条边 e1 和 e2。这会产生两种情况：

• 情况 A：两条边切割出的子树不相交
  • 假设切割 e1 分离出子树 T1，其异或和为 x1。
  • 切割 e2 分离出子树 T2，其异或和为 x2。
  • T1 和 T2 没有公共节点。
  • 此时，三个组件的异或和分别是：x1，x2，以及剩余部分的 total_xor ^ x1 ^ x2。
• 情况 B：一条边切割出的子树包含另一条边切割出的子树
  • 假设切割 e1 分离出子树 T1，异或和为 x1。
  • 切割 e2 的位置在 T1 内部，分离出了一个更小的子树 T2，异或和为 x2。
  • 此时，三个组件的异或和分别是：
    1. x2 (小T2子树)
    2. x1 ^ x2 (T1 除去 T2 的部分)
    3. total_xor ^ x1 (整棵树除去 T1 的部分)

我们可以通过一个 O(N^2) 的双重循环来遍历所有可能的切割组合。

1. 初始化一个非常大的值 min_score = infinity。
2. 外层循环：遍历所有非根节点 i（从 1 到 n-1）。这代表第一次切割，分离出以 i 为根的子树，其异或和为 x1 = xor_sum[i]。
3. 内层循环：遍历所有非根节点 j (且 j != i)。这代表第二次切割，分离出以 j 为根的子树，其异或和为 x2 = xor_sum[j]。
4. 判断拓扑关系：判断子树 i 和子树 j 的关系。
   • 如果 j 是 i 的后代（j 在 i 的子树内），则为情况 B。三个值为 [x2, x1^x2, total_xor^x1]。
   • 如果 i 是 j 的后代（i 在 j 的子树内），则为情况 B。三个值为 [x1, x2^x1, total_xor^x2]。
   • 否则，它们不相交，为情况 A。三个值为 [x1, x2, total_xor^x1^x2]。
5. 计算分数：对于每一种情况，计算 max(vals) - min(vals)，并用它来更新 min_score。
6. 循环结束后，min_score 就是最终答案。

如何判断一个节点是否是另一个节点的后代？ 在最初的 DFS 过程中，我们可以记录每个节点的父节点 parent[u]。然后，要判断 j 是否是 i 的后代，我们可以从 j 开始不断向上跳 parent，看是否能到达 i。

实现

实现细节

• 数据结构:
  • adj: 使用 vector<vector<int>> 作为邻接表来存储树的结构。
  • xor_values: 一个 vector<int> 用来存储在DFS后序遍历中计算出的每个节点为根的子树的异或和。
  • tin, tout: 两个 vector<int> 用来存储DFS过程中的“进入时间”和“离开时间”。这是判断节点间祖先-后代关系的利器。如果节点 u 是节点 v 的祖先，那么 tin[u] <= tin[v] 且 tout[v] <= tout[u]。
• DFS (深度优先搜索):
  • 实现一个 dfs 函数，它从根节点（我们选定0）出发遍历整棵树。
  • 在后序遍历的位置（即访问完一个节点的所有子节点后），计算该节点为根的子树的异或和。
  • 同时，在DFS过程中记录每个节点的 tin 和 tout 时间戳。
• 主逻辑:
  • 首先，调用 dfs 完成预处理，计算出所有子树的异或和以及时间戳。
  • 然后，使用两层嵌套循环，遍历所有可能的两个不同切割点 i 和 j（i 和 j 均不为根节点0）。
  • 对于每一对 (i, j)，利用 tin 和 tout 判断它们的子树是嵌套关系还是不相交关系。
  • 根据不同的拓扑关系，计算出三个组件的异或和。
  • 最后，根据这三个异或和计算当前方案的分数 max - min，并更新全局的最小分数。

代码实现

class Solution {
public:
    int n;                                  // 存储节点的总数
    vector<vector<int>> adj;                // 邻接表，用于存储树的结构
    vector<int> xor_values;                 // 存储以每个节点为根的子树的异或和
    vector<int> tin, tout;                  // tin: DFS进入时间戳, tout: DFS离开时间戳
    int timer;                              // 全局计时器，用于生成时间戳

    /**
     * @brief 深度优先搜索函数
     * @param u 当前访问的节点
     * @param p u 的父节点，用于防止在树中往回走
     * @param nums 原始的节点值数组
     */
    void dfs(int u, int p, const vector<int>& nums) {
        // 记录进入节点u的时间
        tin[u] = timer++;
        // 初始化当前子树的异或和为节点u自身的值
        xor_values[u] = nums[u];
        
        // 遍历u的所有邻居节点v
        for (int v : adj[u]) {
            // 如果邻居是父节点，则跳过，避免死循环
            if (v == p) continue;
            // 递归地对子节点v进行深度优先搜索
            dfs(v, u, nums);
            // 后序遍历位置：在子节点v的子树完全处理完毕后，
            // 将其子树的异或和累加到父节点u的异或和中
            xor_values[u] ^= xor_values[v];
        }
        // 记录离开节点u的时间
        tout[u] = timer++;
    }

    /**
     * @brief 辅助函数，判断节点u是否是节点v的祖先
     * 如果u是v的祖先，那么u的进入时间一定早于等于v，且v的离开时间一定早于等于u
     * @param u 可能的祖先节点
     * @param v 可能的后代节点
     * @return 如果u是v的祖先，则返回true，否则返回false
     */
    bool is_ancestor(int u, int v) {
        return tin[u] <= tin[v] && tout[v] <= tout[u];
    }

    int minimumScore(vector<int>& nums, vector<vector<int>>& edges) {
        // 初始化成员变量
        n = nums.size();
        adj.assign(n, vector<int>());
        xor_values.assign(n, 0);
        tin.assign(n, 0);
        tout.assign(n, 0);
        timer = 0;

        // 步骤 1: 根据edges构建邻接表
        for (const auto& edge : edges) {
            adj[edge[0]].push_back(edge[1]);
            adj[edge[1]].push_back(edge[0]);
        }

        // 步骤 2: 执行DFS进行预处理
        // 假设0为根节点，其父节点设为-1（一个不存在的节点）
        dfs(0, -1, nums);

        // 初始化最小分数为一个非常大的整数
        int min_score = INT_MAX;
        // 整棵树所有节点值的异或和，就是根节点0的子树异或和
        int total_xor = xor_values[0];

        // 步骤 3: 遍历所有可能的两条边切割方案
        // 我们通过遍历所有非根节点对 (i, j) 来模拟切割不同的两条边
        // 循环从1开始，因为节点0是根，切断它没有意义
        for (int i = 1; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                // 定义三个连通组件的异或和
                int val1, val2, val3;

                // 判断 i 和 j 对应子树的拓扑关系
                if (is_ancestor(i, j)) {
                    // 情况B: j 的子树在 i 的子树内部
                    // 切割 (parent(i), i) 和 (parent(j), j)
                    val1 = xor_values[j];                      // 组件1: 子树 j
                    val2 = xor_values[i] ^ xor_values[j];    // 组件2: 子树 i 除去子树 j 的部分
                    val3 = total_xor ^ xor_values[i];        // 组件3: 整棵树除去子树 i 的部分
                } else if (is_ancestor(j, i)) {
                    // 情况B: i 的子树在 j 的子树内部
                    val1 = xor_values[i];                      // 组件1: 子树 i
                    val2 = xor_values[j] ^ xor_values[i];    // 组件2: 子树 j 除去子树 i 的部分
                    val3 = total_xor ^ xor_values[j];        // 组件3: 整棵树除去子树 j 的部分
                } else {
                    // 情况A: i 和 j 的子树不相交
                    val1 = xor_values[i];                      // 组件1: 子树 i
                    val2 = xor_values[j];                      // 组件2: 子树 j
                    val3 = total_xor ^ xor_values[i] ^ xor_values[j]; // 组件3: 剩下的部分
                }

                // 计算当前方案的分数（最大异或值 - 最小异或值）
                int current_max = max({val1, val2, val3});
                int current_min = min({val1, val2, val3});
                
                // 更新全局最小分数
                min_score = min(min_score, current_max - current_min);
            }
        }

        // 返回找到的最小分数
        return min_score;
    }
};

复杂度分析

• 时间复杂度: O(N^2)。
  • 构建邻接表：O(N)。
  • DFS 预处理：O(N)。
  • 双重循环遍历所有切割组合：O(N^2)。在循环内部，判断后代关系最多需要 O(N)（最坏情况是链表），计算分数是 O(1)。所以总体是 O(N^2) 或 O(N^3)，取决于后代判断的实现。为了保证 O(N^2)，后代判断需要优化，本解法使用DFS记录每个子树的节点范围（时间戳法），这样可以在 O(1) 内判断。
• 空间复杂度: O(N)。
  • 用于存储邻接表、父节点数组和子树异或和数组。