题目

给你两个整数 m 和 n 表示一个下标从 0 开始的 m x n 网格图。同时给你两个二维整数数组 guards 和 walls ，其中 guards[i] = [rowi, coli] 且 walls[j] = [rowj, colj] ，分别表示第 i 个警卫和第 j 座墙所在的位置。

一个警卫能看到 4 个坐标轴方向（即东、南、西、北）的所有格子，除非他们被一座墙或者另外一个警卫挡住了视线。如果一个格子能被至少一个警卫看到，那么我们说这个格子被保卫了。

请你返回空格子中，有多少个格子是 没被保卫 的。

示例 1：

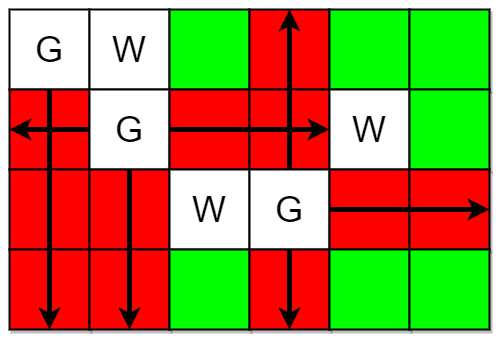
**输入：**m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]] **输出：**7 **解释：**上图中，被保卫和没有被保卫的格子分别用红色和绿色表示。总共有 7 个没有被保卫的格子，所以我们返回 7 。

示例 2：

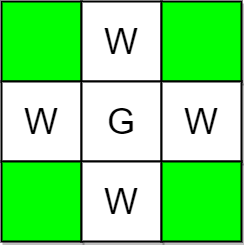
**输入：**m = 3, n = 3, guards = [[1,1]], walls = [[0,1],[1,0],[2,1],[1,2]] **输出：**4 **解释：**上图中，没有被保卫的格子用绿色表示。总共有 4 个没有被保卫的格子，所以我们返回 4 。

提示：

1 <= m, n <= 10^5
2 <= m * n <= 10^5
1 <= guards.length, walls.length <= 5 * 10^4
2 <= guards.length + walls.length <= m * n
guards[i].length == walls[j].length == 2
0 <= rowi, rowj < m
0 <= coli, colj < n
guards 和 walls 中所有位置 互不相同 。

解题思路

这道题最核心的难点在于如何处理重叠的视线。

一个格子可能同时被它上方的警卫和左边的警卫看到。
如果我们遍历每个警卫，去计算“这个警卫能看到多少格子”，然后把所有警卫的结果加起来，就会导致严重的重复计数。

既然“计算”每个警卫的贡献很复杂，我们就应该转换思路：放弃“计算”，转而“模拟”。

我们不去问“这个警卫能看到多少格子？”，而是去问“网格上的每一个格子，它最终的状态是什么？”

这就把问题变成了一个“状态标记”或“地图染色”的问题。

创建一个 $m \times n$ 的二维数组 grid。
我们约定几种状态：
- 0: 空地 (初始状态，未被保卫)
- 1: 已保卫 (被警卫“染上颜色”的空地)
- 2: 障碍物 (墙或警卫，它们会挡住视线)
在模拟视线（染色）之前，我们必须先把所有会“挡住颜料”的东西放到地图上。
遍历 walls 数组，把 grid[r][c] 标记为 2 (障碍物)。
遍历 guards 数组，把 grid[r][c] 也标记为 2 (障碍物)。
- 关键点： 警卫自己也会挡住其他警卫的视线，所以他们也是障碍物。
现在，我们再次遍历 guards 数组（这次是为了让他们“喷射颜料”）。
对于每一个警卫，我们让他向四个方向（东、南、西、北）“喷射”状态 1。
染色规则：
- 颜料（视线）从警卫的下一个格子开始。
- 如果遇到 0 (空地)，就把它染成 1 (已保卫)，然后继续前进。
- 如果遇到 1 (已被保卫)，说明这个格子已经被别的警卫染过了。我们不需要重复计数，但颜料（视线）可以穿过它，继续前进。
- 如果遇到 2 (障碍物)，颜料（视线）被挡住了，停止这个方向的染色。
当所有警卫都完成了“染色”工作后，我们的 grid 地图就有了最终的状态。
此时，我们最后遍历一次地图：
统计所有格子里，状态仍然是 0 (空地) 的格子数量。
这个数量，就是最终“未被保卫”的格子数。

这种“状态模拟”的方法，通过 grid 数组这个媒介，极其巧妙地解决了“视线重叠”的核心问题。

一个格子 [r, c] 无论被多少个警卫的视线扫过，它只会在第一次从 0 变为 1。
之后再有视线扫过它，它的状态保持为 1，不会被错误地累加。
我们最终只关心格子的最终状态 (0 还是 1)，而不是它“被看到了多少次”。

复杂度分析

设 $m$ 为网格行数， $n$ 为网格列数，$G$ 为警卫数量 (len(guards))，$W$ 为墙的数量 (len(walls))。

时间复杂度: $O(m \times n + G + W)$

这个复杂度是线性的，非常高效。我们把它分解来看：

初始化网格 ( $O(m \times n)$ )：
- 创建一个 $m \times n$ 的二维数组 grid，需要 $O(m \times n)$ 的时间。
标记障碍物 ( $O(G + W)$ )：
- 遍历 walls 数组并标记 grid，花费 $O(W)$。
- 遍历 guards 数组并标记 grid，花费 $O(G)$。
模拟视线 ( $O(m \times n)$ )：
- 这是最关键的一步。我们遍历所有 $G$ 个警卫，每个警卫向 4 个方向扫描。
- 正如我们之前详细分析的，虽然外层循环是 $G$ 次，但由于障碍物（墙和警卫）会阻挡视线，每个格子最多只会被来自 4 个方向的扫描各访问一次。
- 因此，这一整步的总工作量上限是 $O(4 \times m \times n)$，即 $O(m \times n)$。
统计结果 ( $O(m \times n)$ )：
- 最后，遍历一次 $m \times n$ 的网格来统计所有状态为 0 的格子，花费 $O(m \times n)$。
- (如果我们使用了优化版的解法，在“染色”时就计数，那么这一步就是 $O(1)$)。

总结：

无论是否优化，总时间复杂度都是：

$O(m \times n) + O(G + W) + O(m \times n) + O(m \times n \text{ or } 1)$

这可以简化为 $O(m \times n + G + W)$。

空间复杂度: $O(m \times n)$

grid 数组：
- 算法的核心开销在于我们创建了一个 $m \times n$ 的二维数组 grid 来存储地图上每个格子的状态。
- 这是必需的，因为它让我们能够正确处理视线的交叉和重叠。
其他：
- directions 数组是 $O(1)$ 的常数空间。
- 没有使用递归，所以没有额外的栈空间开销。

因此，空间复杂度完全由 grid 数组决定，即 $O(m \times n)$。

具体代码

func countUnguarded(m int, n int, guards [][]int, walls [][]int) int {

    // 定义状态
    const (
        EMPTY   = 0 // 空地 (未被保卫)
        GUARDED = 1 // 已被保卫
        OBSTACLE = 2 // 障碍物 (墙 或 警卫)
    )

    // 1. 初始化网格
    grid := make([][]int, m)
    for i := range grid {
        grid[i] = make([]int, n)
    }

    // 2. 放置障碍物 (墙)
    for _, wall := range walls {
        grid[wall[0]][wall[1]] = OBSTACLE
    }

    // 2. 放置障碍物 (警卫)
    for _, guard := range guards {
        grid[guard[0]][guard[1]] = OBSTACLE
    }

    // 定义四个方向: 北, 南, 西, 东
    directions := [][]int{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}

    // 3. 模拟警卫视线 ("染色")
    for _, guard := range guards {
        r, c := guard[0], guard[1]

        for _, dir := range directions {
            dr, dc := dir[0], dir[1]
            // 从警卫的下一个格子开始扫描
            nr, nc := r+dr, c+dc

            // 持续向一个方向扫描，直到出界
            for nr >= 0 && nr < m && nc >= 0 && nc < n {
                // 如果遇到障碍物 (墙或另一个警卫)，停止这个方向的扫描
                if grid[nr][nc] == OBSTACLE {
                    break
                }

                // 如果是空地，标记为 "已被保卫"
                // 如果已经是 GUARDED，保持不变，视线继续穿过
                if grid[nr][nc] == EMPTY {
                    grid[nr][nc] = GUARDED
                }

                // 移动到下一个格子
                nr += dr
                nc += dc
            }
        }
    }

    // 4. 统计结果
    count := 0
    for r := 0; r < m; r++ {
        for c := 0; c < n; c++ {
            // 只计算状态为 EMPTY (0) 的格子
            if grid[r][c] == EMPTY {
                count++
            }
        }
    }

    return count
}

2257. 统计网格图中没有被保卫的格子数

beautifulremi

题目

解题思路

复杂度分析

具体代码