题目

在一个图书馆的长廊里，有一些座位和装饰植物排成一列。给你一个下标从 0 开始，长度为 n 的字符串 corridor ，它包含字母 'S' 和 'P' ，其中每个 'S' 表示一个座位，每个 'P' 表示一株植物。

在下标 0 的左边和下标 n - 1 的右边 已经 分别各放了一个屏风。你还需要额外放置一些屏风。每一个位置 i - 1 和 i 之间（1 <= i <= n - 1），至多能放一个屏风。

请你将走廊用屏风划分为若干段，且每一段内都 恰好有两个座位 ，而每一段内植物的数目没有要求。可能有多种划分方案，如果两个方案中有任何一个屏风的位置不同，那么它们被视为 不同 方案。

请你返回划分走廊的方案数。由于答案可能很大，请你返回它对 109 + 7 取余 的结果。如果没有任何方案，请返回 0 。

示例 1：

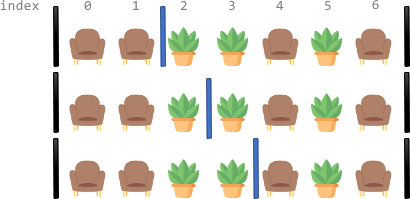
**输入：**corridor = "SSPPSPS" **输出：**3 **解释：**总共有 3 种不同分隔走廊的方案。 上图中黑色的竖线表示已经放置好的屏风。 上图每种方案中，每一段都恰好有 两个 座位。

示例 2：

输入：corridor = "PPSPSP" 输出：1 解释：只有 1 种分隔走廊的方案，就是不放置任何屏风。 放置任何的屏风都会导致有一段无法恰好有 2 个座位。

示例 3：

输入：corridor = "S" 输出：0 解释：没有任何方案，因为总是有一段无法恰好有 2 个座位。

提示：

• n == corridor.length
• 1 <= n <= 10^5
• corridor[i] 要么是 'S' ，要么是 'P' 。

解题思路

这题的关键是：每一段必须恰好 2 个座位，所以所有座位只能按走廊从左到右被“强制”分成一对一对的：第(1,2)个座位一段，第(3,4)个座位一段…… 你能自由选择的，只有相邻两段之间的屏风放在哪。

设走廊里座位总数是 totS：

• 如果 totS == 0：不可能让每段都有 2 个座位 → 0
• 如果 totS 是奇数：总有一段凑不齐 2 个座位 → 0
• 否则可行，并且座位分段方式固定为 (S1,S2) (S3,S4) ...

现在看两段之间的“缝”：

• 第一段的第 2 个座位（S2）和下一段的第 1 个座位（S3）之间可能有若干植物 P
• 假设它们之间有 k 株植物：形如 ... S P P ... P S ...（中间 k 个 P）
• 那么你可以把屏风放在这段间隔的任意“空隙”里：
  • 紧挨着 S2 后面
  • 或者在某个 P 后面
  • 或者紧挨着 S3 前面 一共 k + 1 种位置

而每个间隔的选择彼此独立，所以答案是：

所有相邻段之间的 (k+1) 连乘，对 1e9+7 取模。

一次扫描怎么做（O(n)）

我们从左到右扫描，数到第 2 个座位时，说明完成了一段。 接下来，如果还会有下一段，我们就开始统计这段结束后到下一个座位之间的植物数 plants：

• 当我们遇到下一段的“第 1 个座位”（也就是第 3、5、7…个座位）时： 把答案乘上 (plants + 1)，然后 plants = 0 重新开始。

具体代码

func numberOfWays(corridor string) int {
	const MOD int64 = 1000000007

	// 先统计总座位数
	totalS := 0
	for i := 0; i < len(corridor); i++ {
		if corridor[i] == 'S' {
			totalS++
		}
	}
	if totalS == 0 || totalS%2 == 1 {
		return 0
	}

	var ans int64 = 1
	seats := 0
	plants := 0

	for i := 0; i < len(corridor); i++ {
		if corridor[i] == 'S' {
			seats++
			// 第 3、5、7... 个座位：意味着开始下一段
			// 这时 plants 统计的是上一段结束到这个座位之间的植物数
			if seats > 2 && seats%2 == 1 {
				ans = (ans * int64(plants+1)) % MOD
				plants = 0
			}
		} else { // 'P'
			// 当 seats 是偶数且 >=2：表示刚好完成一段，在等下一段开始
			if seats >= 2 && seats%2 == 0 {
				plants++
			}
		}
	}
	return int(ans)
}