在一个无限的 x 坐标轴上，有许多水果分布在其中某些位置。给你一个二维整数数组 fruits ，其中 fruits[i] = [position_i, amount_i] 表示共有 amount_i 个水果放置在 position_i 上。fruits 已经按 position_i 升序排列 ，每个 position_i 互不相同 。

另给你两个整数 startPos 和 k 。最初，你位于 startPos 。从任何位置，你可以选择 向左或者向右 走。在 x 轴上每移动 一个单位 ，就记作 一步 。你总共可以走 最多 k 步。你每达到一个位置，都会摘掉全部的水果，水果也将从该位置消失（不会再生）。

返回你可以摘到水果的 最大总数 。

示例 1：

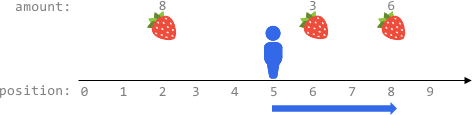
输入：fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4 输出：9 解释： 最佳路线为：

• 向右移动到位置 6 ，摘到 3 个水果
• 向右移动到位置 8 ，摘到 6 个水果 移动 3 步，共摘到 3 + 6 = 9 个水果

示例 2：

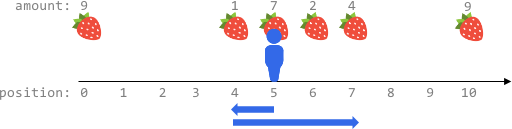
输入：fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4 输出：14 解释： 可以移动最多 k = 4 步，所以无法到达位置 0 和位置 10 。 最佳路线为：

• 在初始位置 5 ，摘到 7 个水果
• 向左移动到位置 4 ，摘到 1 个水果
• 向右移动到位置 6 ，摘到 2 个水果
• 向右移动到位置 7 ，摘到 4 个水果 移动 1 + 3 = 4 步，共摘到 7 + 1 + 2 + 4 = 14 个水果

示例 3：

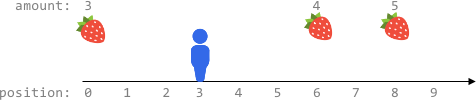
输入：fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2 输出：0 解释： 最多可以移动 k = 2 步，无法到达任一有水果的地方

提示：

• 1 <= fruits.length <= 10^5
• fruits[i].length == 2
• 0 <= startPos, positioni <= 2 * 10^5
• 对于任意 i > 0 ，position_i-1 < position_i 均成立（下标从 0 开始计数）
• 1 <= amount_i <= 104
• 0 <= k <= 2 * 10^5

解题思路

这道题的核心是找到一个水果区间，在满足步数限制 k 的前提下，使得这个区间内的水果总数最大。

问题的关键可以分解为两个部分：

1. 成本计算：对于任意一个想采集的水果区间 [position_i, position_j]，从起点 startPos 出发，采集完这个区间内所有水果所需的最小步数是多少？
2. 寻找最优区间：如何高效地遍历所有可能的区间，找到那个在成本 k 步之内、水果总数最多的区间？

如何计算采集成本

假设我们要采集的连续水果区间的最左端点是 left_pos，最右端点是 right_pos。为了采完这个区间的所有水果，我们必须到达 left_pos 和 right_pos 这两个位置。

从 startPos 出发，到达这两个端点只有两种基本策略：

1. 先往左走，再掉头往右走：路径为 startPos -> left_pos -> right_pos。
2. 先往右走，再掉头往左走：路径为 startPos -> right_pos -> left_pos。

我们需要计算这两种策略的步数，然后取其中较小的一个作为采集该区间的最小成本。

情况分析：

• 策略1: startPos -> left_pos -> right_pos
  • 从 startPos 走到 left_pos 的步数是 startPos - left_pos。
  • 然后从 left_pos 走到 right_pos 的步数是 right_pos - left_pos。
  • 总步数 (成本) = (startPos - left_pos) + (right_pos - left_pos)
• 策略2: startPos -> right_pos -> left_pos
  • 从 startPos 走到 right_pos 的步数是 right_pos - startPos。
  • 然后从 right_pos 走到 left_pos 的步数是 right_pos - left_pos。
  • 总步数 (成本) = (right_pos - startPos) + (right_pos - left_pos)

注意： 上述公式隐含了一个前提，即 left_pos <= startPos <= right_pos。如果 startPos 在区间的外部，情况会更简单：

• 如果 startPos > right_pos (起点在区间的右侧)，那么最佳路径只有一个方向：startPos -> right_pos -> left_pos。总步数就是 startPos - left_pos。
• 如果 startPos < left_pos (起点在区间的左侧)，那么最佳路径也只有一个方向：startPos -> left_pos -> right_pos。总步数就是 right_pos - startPos。

一个统一的、覆盖所有情况的成本计算公式是： cost = (right_pos - left_pos) + min(abs(startPos - left_pos), abs(startPos - right_pos)) 这个公式可以理解为：首先走完整个区间的长度 (right_pos - left_pos)，然后再加上从起点 startPos 走到离它较近的那个端点的距离。

最终，采集区间 [left_pos, right_pos] 的最小成本为：min((startPos - left_pos) + (right_pos - left_pos), (right_pos - startPos) + (right_pos - left_pos)) (在计算时要确保 startPos - left_pos 和 right_pos - startPos 不为负，或直接使用绝对值)。

如何寻找最优区间（滑动窗口）

知道了如何计算任意区间的成本后，我们需要找到那个在 k 步内水果最多的区间。如果暴力枚举所有可能的左右端点组合，时间复杂度会是 O(N2)，对于 N=105 的数据规模来说太慢了。

注意到 fruits 数组是按位置 position 升序排列的，这是一个非常重要的特性，它让我们能使用更高效的算法，比如 滑动窗口。

我们可以把 [left, right] （数组的索引）看作一个“窗口”。我们尝试移动这个窗口，找到最佳的那个。

算法步骤如下：

1. 预处理：计算前缀和 为了能快速计算任意窗口 [left, right] 内的水果总数，我们可以先预处理一个前缀和数组 prefixSum。prefixSum[i] 表示前 i 个位置水果的总和。这样，fruits[left] 到 fruits[right] 的水果总数就可以通过 prefixSum[right+1] - prefixSum[left] 在 O(1) 时间内得到。
2. 初始化滑动窗口
   • 定义左指针 left = 0。
   • 定义一个变量 max_fruits = 0 来记录全局的最大水果数。
3. 移动窗口
   • 用一个 for 循环，让右指针 right 从 0 遍历到 fruits.length - 1。这个 right 指针代表我们当前考虑的采集区间的右边界。
   • 在循环内部，对于当前的窗口 [left, right]：
     • 获取左端点位置 p_left = fruits[left].position 和右端点位置 p_right = fruits[right].position。
     • 使用第一部分推导出的公式计算采集这个区间的成本 cost。
     • 核心逻辑：检查成本是否超标。
       • while (cost > k): 如果当前窗口的成本超过了 k，说明这个窗口太大了，我们需要将其从左边收缩。
       • 将左指针 left 向右移动一位 (left++)，然后重新计算新窗口的成本。
       • 持续这个 while 循环，直到成本 cost <= k 为止。
   • 当 while 循环结束后，当前的窗口 [left, right] 就是以 right 为右端点的、最长的有效窗口。
   • 计算这个有效窗口内的水果总数（使用前缀和），并用它来更新 max_fruits。
   • right 指针进入下一次循环，继续扩大窗口。
4. 返回结果 遍历结束后，max_fruits 中存储的就是最终的答案。

这种方法的时间复杂度是 $O(N)$，因为每个水果最多被 left 和 right 指针访问一次。空间复杂度是 $O(N)$，用于存储前缀和。

具体代码

具体版

class Solution {
public:
    int maxTotalFruits(vector<vector<int>>& fruits, int startPos, int k) {
        
        this -> startPos = startPos;

        int n = fruits.size();

        // 计算前缀和数组,直接用原有数列
        int Sum = 0;

        for(int i = 0; i < n; i++) {
            Sum += fruits[i][1];
            fruits[i][1] = Sum;
        }
        
        // 滑动窗口
        int leftPoint = 0;
        int rightPoint = 0;
        while(rightPoint < n && leftPoint <= rightPoint) {
            if(calculateCost(fruits[leftPoint][0], fruits[rightPoint][0]) <= k) {
                if(leftPoint == 0) {
                    result = max(result, fruits[rightPoint][1]);
                } else {
                    result = max(result, fruits[rightPoint][1] - fruits[leftPoint - 1][1]);
                }
                rightPoint++;
            } else { if(rightPoint == leftPoint) {
                rightPoint++;
            }
                leftPoint++;
            }
        }

        return result;
    }




private:

    int startPos;
    int result = 0;

    int calculateCost(int leftPos, int rightPos) {

        int costToLeft = abs(leftPos - startPos);
        int costToRight = abs(rightPos - startPos);

        return min(costToLeft, costToRight) + abs(leftPos - rightPos);
    }


};

简化版

class Solution {
public:
    int maxTotalFruits(vector<vector<int>>& fruits, int startPos, int k) {
        
        int result = 0;
        int n = fruits.size();

        // 计算前缀和数组,直接用原有数列
        int Sum = 0;

        for(int i = 0; i < n; i++) {
            Sum += fruits[i][1];
            fruits[i][1] = Sum;
        }
        
        // 滑动窗口
        int leftPoint = 0;
        int rightPoint = 0;
        while(rightPoint < n) {
            if(k >= min(abs(fruits[leftPoint][0] - startPos), abs(fruits[rightPoint][0] - startPos)) + abs(fruits[leftPoint][0] - fruits[rightPoint][0])) {
                if(leftPoint == 0) {
                    result = max(result, fruits[rightPoint][1]);
                } else {
                    result = max(result, fruits[rightPoint][1] - fruits[leftPoint - 1][1]);
                }
                rightPoint++;
            } else { if(rightPoint == leftPoint) {
                rightPoint++;
            }
                leftPoint++;
            }
        }
        return result;
    }

};