题目

给你一个 n x n 的整数方阵 matrix 。你可以执行以下操作 任意次 ：

选择 matrix 中相邻两个元素，并将它们都乘以 -1 。

如果两个元素有 公共边 ，那么它们就是相邻的。

你的目的是 最大化 方阵元素的和。请你在执行以上操作之后，返回方阵的最大和。

示例 1：

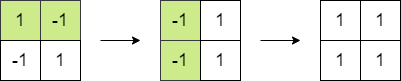
输入：matrix = [[1,-1],[-1,1]] 输出：4 解释：我们可以执行以下操作使和等于 4 ：

将第一行的 2 个元素乘以 -1 。
将第一列的 2 个元素乘以 -1 。

示例 2：

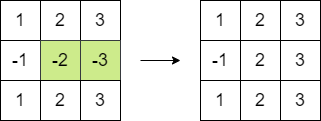
输入：matrix = [[1,2,3],[-1,-2,-3],[1,2,3]] 输出：16 解释：我们可以执行以下操作使和等于 16 ：

将第二行的最后 2 个元素乘以 -1 。

提示：

n == matrix.length == matrix[i].length
2 <= n <= 250
-10^5 <= matrix[i][j] <= 10^5

解题思路

题目说：选相邻两个数，都乘以 -1。这个操作其实隐藏了两个效果：

1. 负号是可以“移动”的

假设数组是 [1, -1, 1]。我想把中间的负号移到最右边，怎么办？

我对后两个数 (-1, 1) 操作 -> 变成 (1, -1)。
数组变成了 [1, 1, -1]。

结论：只要矩阵是连通的，我们可以把一个负号从矩阵的任意位置，一路“推”到任意其他位置。

2. 负号是可以“隔空抵消”的

假设数组是 [-1, 1, 1, -1]（两个负号离得很远）。我想消除这两个负号，怎么办？

我先把第一个负号一路“推”过去，推到最后一个负号的隔壁。
现在它们相邻了，比如变成了 [1, 1, -1, -1]。
我再对这两个相邻的负号操作一次 -> 大家都变成了正数。

结论：只要矩阵里有两个负号，不管它们离多远，我们总能通过一系列操作把它们凑到一起消掉。

基于上面的两个结论，我们发现我们拥有了掌控全局的能力。我们唯一的限制就是：每次操作涉及两个数。这意味着我们改变负数个数时，每次只能 +2 或 -2。

所以，负数个数的奇偶性是永远不会变的（奇数减2还是奇数，偶数减2还是偶数）。

这就引出了两种最终结局：

结局 A：矩阵里原本有“偶数”个负数

策略：既然有偶数个，我们可以两两配对。
操作：把它们两两凑到一起，全部抵消。
结果：我们能让矩阵里所有的数都变成正数（绝对值）。
计算：直接把所有数的绝对值加起来。

结局 B：矩阵里原本有“奇数”个负数

策略：不管怎么消，最后一定会剩下一个负号孤零零的，怎么也消不掉。
思考：既然必须剩下一个负号，而且我们可以把负号“移动”到任意位置，那我们要让谁来背这个锅？
抉择：为了让总和最大，我们必须牺牲那个绝对值最小的数，让它变成负数。
- 注意：这个“牺牲品”不一定非要是原本就是负数的那个数。只要它是全矩阵绝对值最小的，我们就把唯一的负号转移给它。
计算：(所有数的绝对值之和) - 2 * (全矩阵最小的绝对值)。
- 为什么要减 2 倍？ 因为本来把它算作正的加进去了（sum），现在它变成了负的。从 $+x$ 变成 $-x$，总和减少了 $2x$。

如果矩阵里有 0 怎么办？

其实 0 就是绝对值最小的数（$|0|=0$）。
如果原本负数个数是奇数，我们把那个消不掉的负号移到 0 身上。
$-0$ 还是 $0$。
这相当于负号直接消失了！
结论：只要有 0，无论负数有多少个，最后都能变成全是非负数（和最大）。

有了上面的推理，写代码的逻辑就顺理成章了：

全加起来：不管正负，先把所有数的绝对值累加到 sum 中（假设最理想情况）。
找最小值：一边遍历，一边记录矩阵中绝对值最小的那个数 min_num（为了应对奇数个负数的最坏情况）。
数负数：统计原始矩阵中有多少个负数。
最终审判：
- 如果是偶数个负数：直接返回 sum（完美结局）。
- 如果是奇数个负数：必须有一个数作出牺牲，返回 sum - 2 * min_num。

具体代码

func maxMatrixSum(matrix [][]int) int64 {

    Abs := func(x int) int {
        if x < 0 {
            return -x
        }
        return x
    }

    var sum int64 = 0
    var min_num int = 100000
    var neg_count bool = true

    for i := range matrix {
        for j := range matrix[i] {

            k := Abs(matrix[i][j])

            sum += int64(k)

            if k < min_num {
                min_num = k
            }

            if matrix[i][j] <= 0 {
                neg_count = !neg_count
            }
        }
    }

    if neg_count {
        return sum
    } else {
        return sum - 2 * int64(min_num)
    }
}

1975. 最大方阵和

beautifulremi

题目