题目

一个 k x k 的幻方指的是一个 k x k 填满整数的方格阵，且每一行、每一列以及两条对角线的和 全部****相等 。幻方中的整数 不需要互不相同 。显然，每个 1 x 1 的方格都是一个幻方。

给你一个 m x n 的整数矩阵 grid ，请你返回矩阵中 最大幻方 的尺寸（即边长 k）。

示例 1：

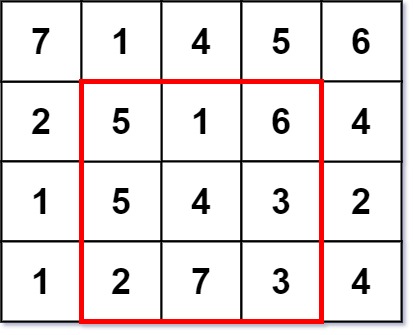
输入：grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]] 输出：3 解释：最大幻方尺寸为 3 。每一行，每一列以及两条对角线的和都等于 12 。

每一行的和：5+1+6 = 5+4+3 = 2+7+3 = 12
每一列的和：5+5+2 = 1+4+7 = 6+3+3 = 12
对角线的和：5+4+3 = 6+4+2 = 12

示例 2：

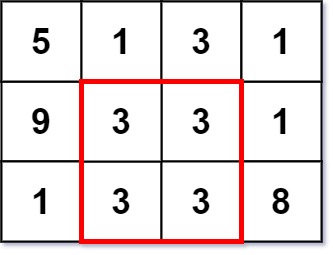
输入：grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]] 输出：2

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 50
1 <= grid[i][j] <= 10^6

解题思路

这道题本质上是一个 “二维区间查询” (2D Range Query) + “搜索策略优化” 的问题。

复杂度分析

题目要求：在 $m \times n$ 的矩阵中，找到最大的正方形子矩阵，使得其行、列、对角线和相等。

如果直接暴力模拟（Brute Force）：

枚举边长 $k$：$O(\min(m,n))$。
枚举左上角 $(i, j)$：$O(m \cdot n)$。
验证幻方：
- 求 $k$ 行之和：需遍历 $k \times k$ 个元素。
- 求 $k$ 列之和：需遍历 $k \times k$ 个元素。
- 单次验证复杂度：$O(k^2)$。

总复杂度：$\sum k^2 \cdot (m \cdot n) \approx O(m \cdot n \cdot \min(m, n)^3)$。

当 $N=50$ 时，$50^5 \approx 3 \times 10^8$，接近超时边缘，且非常低效。

核心瓶颈：每次验证幻方时，都要重复计算大量的子数组和。我们需要把 $O(k^2)$ 的验证降级。

为了加速区间求和，我们引入前缀和 (Prefix Sum)。

虽然可以用二维前缀和（积分图），但针对这道题，我们分别维护 “行前缀和” 和 “列前缀和” 会让逻辑更清晰，且内存访问更连续。

1. 数据结构设计

rowSum[i][j]：第 $i$ 行，前 $j$ 个元素的累加和。
- 查询第 $i$ 行区间 $[c, c+k-1]$ 的和：rowSum[i][c+k] - rowSum[i][c]。
- 时间复杂度：$O(1)$。
colSum[i][j]：第 $j$ 列，前 $i$ 个元素的累加和。
- 查询第 $j$ 列区间 $[r, r+k-1]$ 的和：colSum[r+k][j] - colSum[r][j]。
- 时间复杂度：$O(1)$。

2. 优化后的验证代价

行/列求和：检查 $k$ 行和 $k$ 列，每行/每列只需 $O(1)$。共 $O(k)$。
对角线求和：因为内存不连续，前缀和帮不上忙，必须暴力累加。共 $O(k)$。
优化后单次验证复杂度：$O(k^2) \rightarrow \mathbf{O(k)}$。

总复杂度降为：$O(m \cdot n \cdot \min(m, n)^2)$。对于 $N=50$，计算量级在 $10^6$ 左右，非常安全。

有了工具（前缀和），还需要好的策略（算法流程）来进一步提速。

策略

1. 贪心倒序枚举

题目问的是“最大”尺寸。

策略：$k$ 从 $\min(m, n)$ 开始，从大到小 递减枚举。
收益：一旦找到第一个合法的 $k$，它一定是全局最大的。直接 return k，无需继续计算更小的尺寸。这是处理“最大化问题”的标准贪心策略。

2. 强力剪枝：对角线优先

既然无论如何都要花 $O(k)$ 的时间去算对角线（无法用前缀和优化），那它就是验证流程中“成本最高”且“必须支付”的一环。

策略：先把对角线算出来。
逻辑：
1. 如果主对角线 $\neq$ 副对角线，直接 Pass（无需查前缀和）。
2. 如果相等，设该值为 target，再去查行和列。这相当于加了一个高效率的过滤器，过滤掉绝大部分不合格的方块。

3. 交替验证

在验证行和列时：

不要一口气验完所有行，再验所有列。
策略：验第 0 行 -> 验第 0 列 -> 验第 1 行 -> 验第 1 列...
收益：如果矩阵不是幻方，往往某一行或某一列会出错。交替验证能更早地触发“失败退出”。

具体代码

func largestMagicSquare(grid [][]int) int {
    m, n := len(grid), len(grid[0])

    // 1. 预处理 rowSum 和 colSum
    // rowSum[i][j] 代表第 i 行，前 j 个数的和
    rowSum := make([][]int, m)
    for i := range rowSum {
        rowSum[i] = make([]int, n+1)
        for j := 0; j < n; j++ {
            rowSum[i][j+1] = rowSum[i][j] + grid[i][j]
        }
    }

    // colSum[i][j] 代表第 j 列，前 i 个数的和
    colSum := make([][]int, m+1)
    for i := range colSum {
        colSum[i] = make([]int, n)
    }
    for j := 0; j < n; j++ {
        for i := 0; i < m; i++ {
            colSum[i+1][j] = colSum[i][j] + grid[i][j]
        }
    }

    // 2. 倒序枚举尺寸 k (从大到小)
    // 这样只要找到第一个符合条件的，就是最大的，直接 return
    for k := min(m, n); k > 1; k-- {
        // 枚举左上角位置 (i, j)
        for i := 0; i+k <= m; i++ {
            nextPos:
            for j := 0; j+k <= n; j++ {
                
                // 3. 剪枝核心：优先检查对角线
                // 因为对角线没有前缀和可用，必须遍历。如果对角线不对，
                // 就没必要去查 rowSum/colSum 了，这比 total%k 更直接。
                d1, d2 := 0, 0
                for p := 0; p < k; p++ {
                    d1 += grid[i+p][j+p]
                    d2 += grid[i+p][j+k-1-p]
                }
                
                if d1 != d2 {
                    continue // 对角线不相等，剪枝
                }
                
                target := d1 // 每一行、每一列的目标和

                // 4. 验证行与列 (交替验证，发现错误立即退出)
                for p := 0; p < k; p++ {
                    // 检查第 p 行: rowSum区间 [j, j+k]
                    rs := rowSum[i+p][j+k] - rowSum[i+p][j]
                    if rs != target {
                        continue nextPos
                    }

                    // 检查第 p 列: colSum区间 [i, i+k]
                    // 注意：colSum 的第一维是行索引，第二维是列索引
                    cs := colSum[i+k][j+p] - colSum[i][j+p]
                    if cs != target {
                        continue nextPos
                    }
                }

                // 如果所有检查都通过
                return k
            }
        }
    }

    return 1
}

1895. 最大的幻方

beautifulremi

题目