题目

Alice 把 n 个气球排列在一根绳子上。给你一个下标从 0 开始的字符串 colors ，其中 colors[i] 是第 i 个气球的颜色。

Alice 想要把绳子装扮成 五颜六色的 ，且她不希望两个连续的气球涂着相同的颜色，所以她喊来 Bob 帮忙。Bob 可以从绳子上移除一些气球使绳子变成彩色。给你一个 下标从 0 开始 的整数数组 neededTime ，其中 neededTime[i] 是 Bob 从绳子上移除第 i 个气球需要的时间（以秒为单位）。

返回 Bob 使绳子变成彩色需要的 最少时间 。

示例 1：

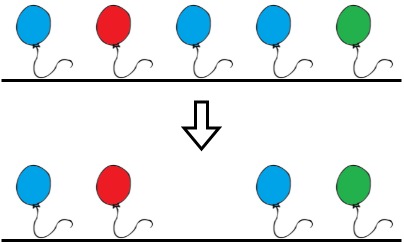
输入：colors = "abaac", neededTime = [1,2,3,4,5] 输出：3 解释：在上图中，'a' 是蓝色，'b' 是红色且 'c' 是绿色。 Bob 可以移除下标 2 的蓝色气球。这将花费 3 秒。移除后，不存在两个连续的气球涂着相同的颜色。总时间 = 3 。

示例 2：

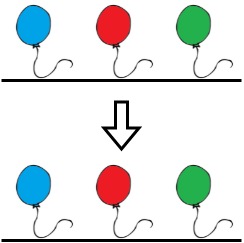
输入：colors = "abc", neededTime = [1,2,3] 输出：0 解释：绳子已经是彩色的，Bob 不需要从绳子上移除任何气球。

示例 3：

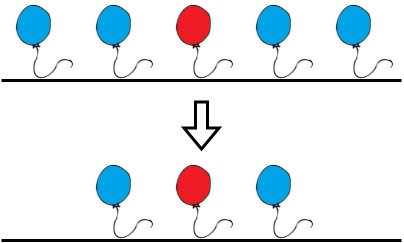
输入：colors = "aabaa", neededTime = [1,2,3,4,1] 输出：2 解释：Bob 会移除下标 0 和下标 4 处的气球。这两个气球各需要 1 秒来移除。移除后，不存在两个连续的气球涂着相同的颜色。总时间 = 1 + 1 = 2 。

提示：

n == colors.length == neededTime.length
1 <= n <= 10^5
1 <= neededTime[i] <= 10^4
colors 仅由小写英文字母组成

解题思路

问题： 绳子上有n个气球，colors[i] 是颜色，neededTime[i] 是移除的代价。
目标： 移除总时间最少的气球，使得没有两个相邻的气球颜色相同。
最小代价： 这两个词（“最少时间”、“没有两个相邻”）强烈暗示了这是一个贪心算法或动态规划问题。我们通常先尝试贪心，因为它更简单。
问题的唯一约束是 colors[i] == colors[i+1]。
一个 abc 这样的字符串是完全OK的，不需要任何操作，代价为 0。
一个 aabaa 这样的字符串，有两个问题点：aa (下标 0-1) 和 aa (下标 3-4)。
一个 aaaac 这样的字符串，有三个问题点：a[0]==a[1], a[1]==a[2], a[2]==a[3]。

让我们专注于一个连续相同颜色的“组”。比如 ...b[aaa]c... (这里的 [aaa] 是一个连续的 'a' 组)。

子问题： 对于这个 [aaa] 组，我们必须对它进行操作，直到它不再有相邻的 'a'。
策略分析：
1. 我们可以把三个 'a' 全都移除。
2. 我们可以移除任意两个 'a'，只留下一个。
3. 我们不能只移除一个 'a'，因为还会剩下 aa，仍然违规。
结论： 对于一个由 $k$ 个相同颜色气球组成的连续组，我们必须移除 $k-1$ 个，只留下一个（或者 $k$ 个全移除，但这显然代价更高）。
最小代价决策：
- 我们必须移除 $k-1$ 个气球。
- 为了使移除的总时间最少，我们显然应该保留那个移除代价最大的气球。
- 因此，处理这一个“组”的最小代价 = (这个组所有气球的时间总和) - (这个组中代价最大的那个气球的时间)。
整个字符串 colors 可以被看作是由 1 个或多个“连续相同颜色的组”构成的。
- 例如："aabaa" -> ["aa", "b", "aa"]
- 例如："abaac" -> ["a", "b", "aa", "c"]
关键洞察： 对任何一个组（比如 [aa]）做的决策，完全不影响对其他组（比如 [b] 或 [c]）的决策。它们是独立的子问题。
全局最优解： 既然子问题是独立的，那么全局的最小总时间 = 所有“组”的最小代价之和。

现在我们有了两种等价的实现思路：

思路 A：直接累加“要移除的”时间（最直观的贪心）

这个思路是“正向思维”：我们只计算那些 必须被扔掉 的气球的时间。

初始化 total_cost = 0。
遍历气球数组，但我们要识别“组”。
我们使用一个指针 i 遍历，同时维护一个 max_cost_in_group（当前组的最大代价）。
从 i = 0 开始，max_cost_in_group = neededTime[0]。
从 i = 1 开始循环：
- 情况 1：colors[i] == colors[i-1] (我们还在同一个组里)
  - 我们遇到了一个冲突。必须移除一个。移除哪个？移除代价较小的那个。
  - total_cost += min(max_cost_in_group, neededTime[i])
  - 关键： 移除后，“幸存”下来参与下一次比较的，一定是那个代价更大的。所以我们必须更新“幸存者”的代价。
  - max_cost_in_group = max(max_cost_in_group, neededTime[i])
- 情况 2：colors[i] != colors[i-1] (上一个组结束了，新组开始了)
  - 上一个组的计算已经（在之前的步骤中）全部完成了。
  - 我们只需要为这个新组重置 max_cost_in_group。
  - max_cost_in_group = neededTime[i]
循环结束后，total_cost 就是答案。

思路 B：总时间 - “要保留的”时间（你的思路）

这个思路是“逆向思维”，它利用了第 3 步的公式：组代价 = 组总和 - 组最大值。

全局代价 = $\sum (\text{所有组的代价})$
全局代价 = $\sum (\text{组总和} - \text{组最大值})$
根据分配律：全局代价 = $\sum (\text{组总和}) - \sum (\text{组最大值})$
分析这两部分：
- $\sum (\text{组总和})$：把所有组的总和加起来，不就是所有气球的总时间（neededTimeSum）吗？
- $\sum (\text{组最大值})$：这就是所有组中，那个应该被保留的“最大代价”气球的总和（你代码中的 sum_max）。
算法：
1. 计算 neededTimeSum (所有气球的总时间)。
2. 计算 sum_max (所有“连续相同颜色组”中，各自的最大代价之和)。
3. 返回 neededTimeSum - sum_max。

具体代码

func minCost(colors string, neededTime []int) int {

    n := len(neededTime)

    last := colors[0]
    cur := colors[0]
    max := neededTime[0]
    sum_max := 0

    // 找出每个重复序列的最大值
    for i := 1; i < n; i++ {
        last, cur = cur, colors[i]
        if cur != last {
            sum_max += max
            max = neededTime[i]
        } else {
            if neededTime[i] > max {
                max = neededTime[i]
            }
        }
    }

    sum_max += max

    neededTimeSum := 0
    for _, num := range neededTime {
        neededTimeSum += num
    }

    return neededTimeSum - sum_max

}

1578. 使绳子变成彩色的最短时间

beautifulremi

题目

解题思路

思路 A：直接累加“要移除的”时间（最直观的贪心）

思路 B：总时间 - “要保留的”时间（你的思路）

具体代码