题目

超市正在促销，你可以用 numExchange 个空水瓶从超市兑换一瓶水。最开始，你一共购入了 numBottles瓶水。

如果喝掉了水瓶中的水，那么水瓶就会变成空的。

给你两个整数 numBottles 和 numExchange ，返回你 最多 可以喝到多少瓶水。

示例 1：

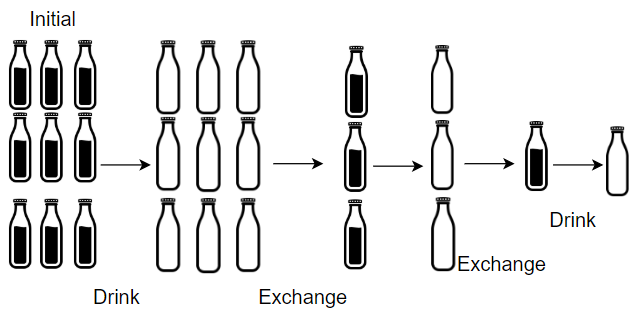
输入：numBottles = 9, numExchange = 3 输出：13 解释：你可以用 3 个空瓶兑换 1 瓶水。 所以最多能喝到 9 + 3 + 1 = 13 瓶水。

示例 2：

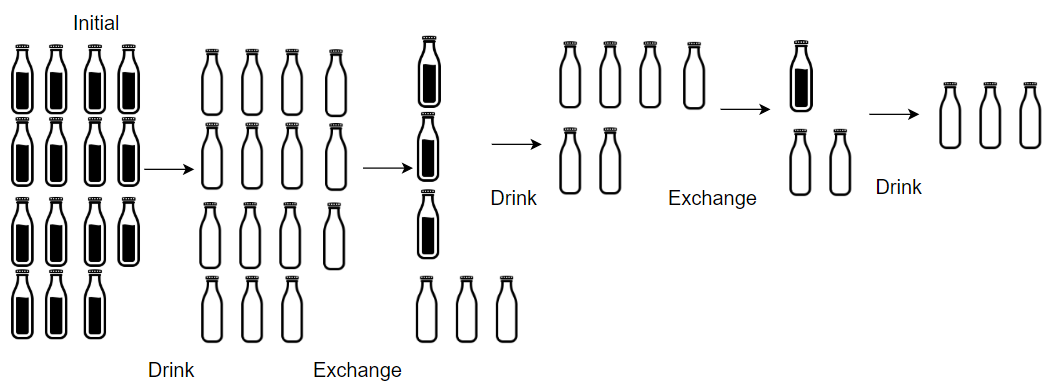
输入：numBottles = 15, numExchange = 4 输出：19 解释：你可以用 4 个空瓶兑换 1 瓶水。 所以最多能喝到 15 + 3 + 1 = 19 瓶水。

提示：

• 1 <= numBottles <= 100
• 2 <= numExchange <= 100

解题思路

思路一：模拟过程

最直接的想法就是完整地模拟整个换水喝的过程。我们只需要跟踪两个核心变量：

1. 已经喝掉的水瓶总数 (totalDrank)
2. 当前拥有的空水瓶数量 (emptyBottles)

解题步骤如下：

1. 初始化：
   • 你最开始买了 numBottles 瓶水，所以你肯定能喝掉这 numBottles 瓶。
   • 因此，totalDrank 的初始值就是 numBottles。
   • 喝完这些水后，你就拥有了 numBottles 个空水瓶。
   • 因此，emptyBottles 的初始值也是 numBottles。
2. 循环兑换：
   • 只要你手里的空水瓶数量 emptyBottles 大于或等于 numExchange，你就一直可以进行兑换。
   • 在循环内部：
     • 计算这一次能兑换多少瓶新水：newBottles = emptyBottles / numExchange (这里是整数除法，只取商)。
     • 将新换来的水喝掉，更新喝水总量：totalDrank += newBottles。
     • 更新你手中的空水瓶数量。你原来的空水瓶用掉了一部分，但新喝完的水又变成了新的空水瓶。所以，新的空水瓶数量 = 换完剩下的 + 新喝完的。
       • 换完剩下的：emptyBottles % numExchange
       • 新喝完的：newBottles
       • 所以，emptyBottles = (emptyBottles % numExchange) + newBottles。
3. 结束循环：
   • 当 emptyBottles 小于 numExchange 时，你再也无法兑换新的一瓶水了，循环结束。
   • 此时的 totalDrank 就是最终答案。

思路二：数学方法

我们可以换个角度思考这个问题。

• 你最初有 numBottles 瓶水可以喝。
• 之后每多喝一瓶水，都是通过兑换得来的。
• 兑换一瓶新水，你需要付出 numExchange 个空瓶，但喝完后你又能拿回 1 个空瓶。所以，每成功兑换一瓶新水，你净损失的空瓶数量是 numExchange - 1。

那么问题就变成了：你最初拥有的 numBottles 个空瓶，总共能承受多少次“净损失 numExchange - 1”的操作？

这里有一个小小的陷阱：你不能用完最后一个空瓶，因为你需要用它来参与最后的兑换。可以这样理解，你总共有 numBottles 个空瓶，但其中 1 个是不能被“净损失”掉的（它是流转的“本金”），所以你真正能用来“净损失”的空瓶只有 numBottles - 1 个。

所以，你能额外兑换到的水瓶数量就是：

$$\text{额外兑换数}=\lfloor\frac{\text{numBottles}-1}{\text{numExchange}-1}\rfloor$$

(向下取整，因为你不能兑换小数瓶水)

最终你能喝到的总数就是：

总数=初始水瓶数+额外兑换数

$$\text{总数}=\text{numBottles}+\lfloor\frac{\text{numBottles}-1}{\text{numExchange}-1}\rfloor$$

在大多数编程语言中，整数除法自动就是向下取整，所以公式可以写成： totalDrank = numBottles + (numBottles - 1) / (numExchange - 1)

具体代码

func numWaterBottles(numBottles int, numExchange int) int {

    ans := 0
    emptyBottles := 0
    for numBottles != 0 {
        ans += numBottles
        numBottles, emptyBottles = (numBottles + emptyBottles) / numExchange, (numBottles + emptyBottles) % numExchange
    }
    return ans
}