题目
给你一个 m x n 的二进制矩阵 mat ,请你返回有多少个 子矩形 的元素全部都是 1 。
示例 1:
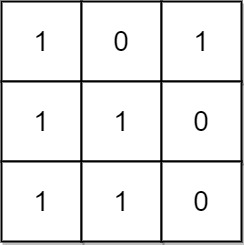
输入:mat = [[1,0,1],[1,1,0],[1,1,0]] 输出:13 解释: 有 6 个 1x1 的矩形。 有 2 个 1x2 的矩形。 有 3 个 2x1 的矩形。 有 1 个 2x2 的矩形。 有 1 个 3x1 的矩形。 矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。
示例 2:
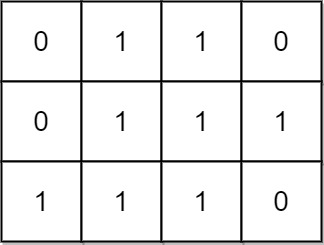
输入:mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]] 输出:24 解释: 有 8 个 1x1 的子矩形。 有 5 个 1x2 的子矩形。 有 2 个 1x3 的子矩形。 有 4 个 2x1 的子矩形。 有 2 个 2x2 的子矩形。 有 2 个 3x1 的子矩形。 有 1 个 3x2 的子矩形。 矩形数目总共 = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24 。
提示:
1 <= m, n <= 150mat[i][j]仅包含0或1
解题思路
这道题是“统计全 1 正方形”的延伸,但难度有所增加,因为它要求统计的是矩形,形状更加灵活。基本思路是将二维问题降维成一维问题来处理。
我们可以遍历矩阵的每一行,对于每一行,我们都计算以当前行作为矩形底边的所有全 1 矩形的数量。把每一行的结果加起来,就是最终的答案。
关键在于,当我们以第 i 行为底边时,如何高效地计算矩形的数量?
1.定义“高度”
为了方便计算,我们引入一个辅助的 height 数组,height 数组的长度与矩阵的列数 n 相同。
height[j] 的含义是:在当前行 i,第 j 列的元素 mat[i][j] 向上数有多少个连续的 1。
- 如果
mat[i][j]是1,那么height[j]的值就是上一行对应位置的高度height[j](旧) + 1。 - 如果
mat[i][j]是0,那么连续性被中断,height[j]直接变为0。
举个例子: mat = [[0,1,1,0], [0,1,1,1], [1,1,1,0]]
- 处理第 0 行:
[0,1,1,0]- 计算出的
height数组为:[0, 1, 1, 0]
- 计算出的
- 处理第 1 行:
[0,1,1,1]mat[1][0]=0->height[0]=0mat[1][1]=1->height[1]=(上一行的height[1])+ 1 = 1 + 1 = 2mat[1][2]=1->height[2]=(上一行的height[2])+ 1 = 1 + 1 = 2mat[1][3]=1->height[3]=(上一行的height[3])+ 1 = 0 + 1 = 1- 计算出的
height数组为:[0, 2, 2, 1]
- 处理第 2 行:
[1,1,1,0]mat[2][0]=1->height[0]=0+1=1mat[2][1]=1->height[1]=2+1=3mat[2][2]=1->height[2]=2+1=3mat[2][3]=0->height[3]=0- 计算出的
height数组为:[1, 3, 3, 0]
2.在一维“高度”数组上计数
现在,问题转化了:对于每一行计算出的 height 数组(你可以把它想象成一个直方图),我们需要计算在这个直方图中能形成多少个矩形。
我们可以在得到每一行的 height 数组后,立刻计算矩形数量。
如何计算呢?我们可以遍历 height 数组,对于每一个 height[j],我们把它作为矩形的右边界,然后向左扩展,看看能形成多少个矩形。
具体算法: 对于当前行的 height 数组:
- 初始化一个
row_count = 0用于统计当前行的矩形数。 - 遍历
j从0到n-1(作为矩形的右边界):- 初始化一个
min_height = height[j]。 - 如果
min_height > 0,我们开始向左遍历k从j到0(作为矩形的左边界):- 更新
min_height = min(min_height, height[k])。因为从k到j这个范围内的所有柱子要形成一个矩形,它的高度不能超过最矮的那个柱子。 - 一旦确定了左边界
k、右边界j和这段区间的最小高度min_height,这意味着我们可以构成min_height个矩形(宽度为j-k+1,高度可以为1, 2, ..., min_height)。 - 将这个数量累加到
row_count中:row_count += min_height。
- 更新
- 初始化一个
- 将
row_count累加到最终的总结果total_count中。
流程总结
- 初始化总矩形数
total_count = 0。 - 创建一个
height数组,大小为n,初始值全为0。 - 外层循环:遍历矩阵的每一行
i从0到m-1。 a. 更新height数组:遍历每一列j从0到n-1,根据mat[i][j]的值更新height[j]。 b. 计算当前行矩形数: i. 内层循环1:遍历j从0到n-1(作为右边界)。 ii. 初始化min_height = height[j]。 iii. 内层循环2:遍历k从j向左到0(作为左边界)。 1. 更新min_height = min(min_height, height[k])。 2.total_count += min_height。 - 所有行遍历完毕后,返回
total_count。
这个算法的时间复杂度是 $O(m * n^2)$,空间复杂度是 $O(n)$,对于 m, n <= 150 的数据规模是完全可以通过的。
具体代码
class Solution {
public:
int numSubmat(vector<vector<int>>& mat) {
int m = mat[0].size(); // 长
int n = mat.size(); // 宽
vector<int> height(m, 0);
int result = 0;
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++) // 更新height数组
{
if(mat[i][j])
height[j]++;
else
height[j] = 0;
}
for(int j = 0; j < m; j++)
{
int minheight = height[j];
for(int k = j; k >= 0; k--) // 把当前height当作右边界
{
if(minheight == 0)
break;
minheight = min(minheight, height[k]);
result += minheight;
}
}
}
return result;
}
};
优化思路
对于每一行,这个算法都用了 $O(n^2)$ 的时间(代码中的 j 和 k 两层循环)来计算由 height 数组构成的矩形数量。
这个 $O(n^2)$ 的计算部分,可以通过单调栈 的思想,优化到 $O(n)$。
O(m * n) 解法思路
我们依然保留外层的主体结构:逐行更新 height 数组。关键是优化更新完 height 数组后的计数过程。
对于当前行 i,我们有 height 数组。我们想在 O(n) 时间内计算出所有以当前行为底边的矩形数量。
我们可以定义一个 count[j],表示以 (i, j) 为右下角的矩形有多少个。那么当前行贡献的总数就是 sum(count[0], count[1], ..., count[n-1])。
现在的问题变成了如何高效计算 count[j]。
观察 count[j] 的构成:它等于 height[j] 加上 “多少个以 (i, j-1) 为右下角的矩形可以向右延伸一格”。
这听起来有点复杂,我们换一个角度:
count[j] = (宽度为1的矩形数量) + (宽度为2的矩形数量) + ...
这个数量可以通过一个递推关系和单调栈来解决。
- 我们从左到右遍历
height数组(j从 0到 m-1)。 - 我们维护一个单调递增栈,栈里存放的是
height数组的下标,这些下标对应的height值是严格递增的。 - 当我们处理到
height[j]时:- 出栈:不断比较
height[j]和栈顶下标对应的height值。如果height[j]小于等于栈顶的高度,说明栈顶那个高柱子形成的矩形区域在这里中断了,需要将栈顶元素弹出。 - 计算:在处理
j时,栈顶的元素(如果存在)就是j左侧第一个比height[j]矮的柱子的下标,我们称之为p。- 这意味着从
p+1到j的所有柱子高度都> a height[p]并且>= height[j]。 - 以
(i, j)为右下角,且高度恰好为h(height[p] < h <= height[j])的矩形,其宽度可以从j一直延伸到p+1。
- 这意味着从
- 递推关系:
- 设
dp[j]是以(i, j)为右下角的矩形数量。 p是j左侧第一个height[p] < height[j]的位置。- 那么,
dp[j]=height[j] * (j - p)(这部分是新形成的、高度大于height[p]的矩形) +dp[p](这部分是之前在p位置就已经算过的、可以延伸过来的矮矩形)。 - 如果
j左侧不存在比它矮的柱子(即p不存在),那么dp[j] = height[j] * (j + 1)。
- 设
- 出栈:不断比较
具体解释
对于每一行,我们都会计算出一个 height 数组。然后,我们需要高效地计算这个 height 数组(直方图)能构成的所有矩形数量。
关键问题: 如何计算以每一根柱子 j 为右下角的矩形有多少个? 如果我们能算出这个值,把它对所有 j 求和,就得到了当前行的总数。我们把这个值称为 dp[j]。
核心思想:矩形的分解
以 j 为右下角的矩形可以分为两大类:
- “新”矩形:这些矩形的高度,受到了
height[j]的“恩惠”,它们的高度h必须依赖height[j]本身,无法在j的左侧单独存在。 - “旧”矩形:这些矩形的高度
h比较矮,它们在j的左侧已经形成,现在只是简单地向右“扩张”了一格而已。
这个区分是理解的关键,递推公式正是建立在这个分解之上的。
dp[j] = (“新”矩形的数量) + (“旧”矩形的数量)
举例说明
假设我们正在处理某一行,计算出的 height 数组是 [1, 3, 2, 4]。
第 1 步: j = 0, height[0] = 1
- 以
(i, 0)为右下角的矩形有哪些?- 只有一个:高度为1,宽度为1的矩形。
- 所以
dp[0] = 1。 - 单调栈
stk(存下标):[0]
第 2 步: j = 1, height[1] = 3
- 以
(i, 1)为右下角的矩形有哪些?- 宽度为1的:高1、高2、高3(共3个)。
- 宽度为2的:
min(height[0], height[1])=min(1, 3)= 1。所以只能有高为1的(共1个)。 - 总数 = 3 + 1 = 4。所以
dp[1] = 4。
- 如何用公式算出来?
j=1左边第一个比它矮的柱子是j=0(我们称之为p=0)。- “新”矩形:这些是高度大于
height[p](即大于1)的矩形。它们的高度可以是2或3,宽度只能是1 (从j=1到p+1=1)。但我们用一个更统一的公式计算:height[j] * (j - p) = 3 * (1 - 0) = 3。这3个矩形是:1x3,1x2,1x1。 - “旧”矩形:这些是高度小于等于
height[p](即等于1)的矩形。它们是从p=0的位置延伸过来的。有多少个呢?正好是dp[p]=dp[0]= 1 个。 dp[1] = (新矩形) + (旧矩形) = 3 + 1 = 4。
- 单调栈
stk:height[1] > height[0],不弹出。[0, 1]
第 3 步: j = 2, height[2] = 2
height[2] = 2比栈顶的height[1] = 3要矮,所以1出栈。- 现在栈顶是
0,height[0] = 1比height[2] = 2矮。 - 所以,
j=2左边第一个比它矮的柱子是j=0(即p=0)。 - 计算
dp[2]:p = 0。- “新”矩形:
height[j] * (j - p) = 2 * (2 - 0) = 4。这4个矩形是:- 宽度为2(从
j=2到p+1=1),高度为1、2。 - 宽度为1(在
j=2处),高度为1、2。
- 宽度为2(从
- “旧”矩形:从
p=0处继承,数量为dp[p]=dp[0]= 1。 dp[2] = (新矩形) + (旧矩形) = 4 + 1 = 5。
- 手动验证:以
j=2为右下角的矩形:宽1高1、宽1高2、宽2高1、宽2高2、宽3高1。确实是5个。 - 单调栈
stk:[0, 2]
第 4 步: j = 3, height[3] = 4
height[3] = 4比栈顶的height[2] = 2高。- 所以,
j=3左边第一个比它矮的柱子是j=2(即p=2)。 - 计算
dp[3]:p = 2。- “新”矩形:
height[j] * (j - p) = 4 * (3 - 2) = 4。 - “旧”矩形:从
p=2处继承,数量为dp[p]=dp[2]= 5。 dp[3] = (新矩形) + (旧矩形) = 4 + 5 = 9。
- 单调栈
stk:[0, 2, 3]
- 对于
height数组[1, 3, 2, 4],我们计算出了dp数组为[1, 4, 5, 9]。 - 这一行贡献的矩形总数就是
1 + 4 + 5 + 9 = 19。
在这个过程中,单调栈的作用是帮助我们在 O(1) 的摊销时间内,迅速找到每个 j 左侧的第一个更矮的柱子 p,从而可以实现动态规划 dp[j] = dp[p] + height[j]*(j-p) 。
优化后的算法流程
- 初始化
总数result = 0,height数组(长度为列数)。 - 遍历每一行
i:- a. 根据
mat[i]更新height数组。 - b. 遍历每一列
j:- i. 用单调栈找到
j左边第一个更矮的位置p。 - ii. 根据公式
dp[j] = dp[p] + height[j] * (j-p)计算以(i, j)为右下角的矩形数。
- i. 用单调栈找到
- c. 将本行所有
dp[j]的值累加到result。
- a. 根据
- 返回
result。
优化后的代码
class Solution {
public:
int numSubmat(std::vector<std::vector<int>>& mat) {
if (mat.empty() || mat[0].empty()) {
return 0;
}
int n = mat.size(); // 获取行数 (rows)
int m = mat[0].size(); // 获取列数 (columns)
int result = 0;
vector<int> height(m, 0);
// 外层循环,逐行处理
for (int i = 0; i < n; ++i) {
// 第一步:更新 height 数组
// height[j] 表示在第 i 行时,第 j 列向上有多少个连续的 1
for (int j = 0; j < m; ++j) {
height[j] = (mat[i][j] == 1) ? height[j] + 1 : 0;
}
// 第二步:使用单调栈在 O(m) 时间内计算当前行的矩形数
// dp[j] 表示以 (i, j) 为右下角的矩形数量
vector<int> dp(m, 0);
stack<int> stk; // 存放下标的单调递增栈
for (int j = 0; j < m; ++j) {
// 维护一个高度递增的单调栈
// 弹出所有比当前 height[j] 高或相等的柱子
while (!stk.empty() && height[stk.top()] >= height[j]) {
stk.pop();
}
// p 是 j 左侧第一个比 height[j] 矮的柱子的下标
int p = stk.empty() ? -1 : stk.top();
int width = j - p;
// 获取 p 位置的 dp 值。如果 p 不存在,说明左边没有更矮的,值为 0
int prev_dp = stk.empty() ? 0 : dp[p];
// 核心递推公式:
// dp[j] = (p位置的dp值) + (新产生的矩形数量)
// 新产生的矩形,是以 height[j] 为最小高度,向左延伸到 p+1 位置构成的
dp[j] = prev_dp + height[j] * width;
// 将当前下标压入栈
stk.push(j);
}
// 第三步:将当前行计算出的所有矩形数累加到总结果中
for (int count : dp) {
result += count;
}
}
return result;
}
};
