题目
你有一个 n x 3 的网格图 grid ,你需要用 红,黄,绿 三种颜色之一给每一个格子上色,且确保相邻格子颜色不同(也就是有相同水平边或者垂直边的格子颜色不同)。
给你网格图的行数 n 。
请你返回给 grid 涂色的方案数。由于答案可能会非常大,请你返回答案对 10^9 + 7 取余的结果。
示例 1:
输入:n = 1 输出:12 解释:总共有 12 种可行的方法:
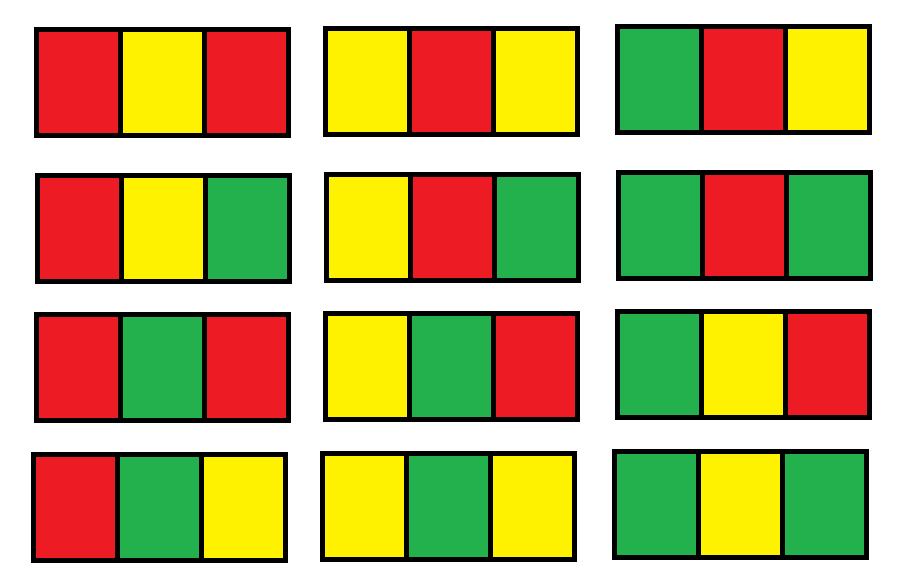
示例 2:
输入:n = 2 输出:54
示例 3:
输入:n = 3 输出:246
示例 4:
输入:n = 7 输出:106494
示例 5:
输入:n = 5000 输出:30228214
提示:
n == grid.lengthgrid[i].length == 31 <= n <= 5000
解题思路
这是一道经典的动态规划(Dynamic Programming)问题。
由于网格的宽度固定为 3,而高度 $n$ 很大,我们无法直接枚举所有格子的颜色。但是,我们可以一行一行地进行涂色,因为第 $i$ 行的合法涂色方案只取决于第 $i-1$ 行的颜色分布。
对于任意一行(有 3 个格子),只要满足“相邻格子颜色不同”,其颜色模式其实只有两种结构类型。我们需要关注的不是具体涂了红、黄、绿哪个颜色,而是第 1 个格子和第 3 个格子的颜色关系。
我们定义两种状态类型:
- Type 0 (ABA模式):这一行的第 1 个格子和第 3 个格子颜色相同。
- 例如:
红-黄-红,绿-蓝-绿。 - (中间格子肯定和两边不同,所以只要头尾相同就是这种模式)。
- 例如:
- Type 1 (ABC模式):这一行的第 1 个格子和第 3 个格子颜色不同。
- 例如:
红-黄-绿,蓝-红-黄。 - (当然,三个格子两两之间都必须满足相邻不同)。
- 例如:
当 $n=1$ 时,我们只看第一行:
- Type 0 (ABA) 的方案数:
- 第 1 格有 3 种选色。
- 第 2 格有 2 种选色(不能和第1格一样)。
- 第 3 格有 1 种选色(必须和第1格一样)。
- 总数 = $3 \times 2 \times 1 = 6$ 种。
- Type 1 (ABC) 的方案数:
- 第 1 格有 3 种选色。
- 第 2 格有 2 种选色。
- 第 3 格有 1 种选色(不能和第2格一样,且因为是ABC模式,也不能和第1格一样)。
- 总数 = $3 \times 2 \times 1 = 6$ 种。
所以,$n=1$ 时总共有 $6+6=12$ 种,符合题目示例。
假设我们已经知道了第 $i-1$ 行属于 ABA 模式的数量是 $a_{i-1}$,属于 ABC 模式的数量是 $b_{i-1}$。我们需要计算第 $i$ 行的数量 $a_i$ 和 $b_i$。
这就需要分析不同模式之间的兼容性(即上下相邻格子颜色不能相同)。
情况 A:如果上一行是 ABA 模式(比如 1-2-1)
下一行可以是哪种模式?
- 转变为 ABA 模式:有 3 种方法。
- 如果上一行是
1-2-1,下一行想变成x-y-x。经过排列组合推导,合法的x-y-x有 3 种(例如2-1-2,2-3-2,3-1-3等,具体推导略)。
- 如果上一行是
- 转变为 ABC 模式:有 2 种方法。
- 如果上一行是
1-2-1,下一行变成x-y-z只有 2 种合法组合。
- 如果上一行是
情况 B:如果上一行是 ABC 模式(比如 1-2-3)
下一行可以是哪种模式?
- 转变为 ABA 模式:有 2 种方法。
- 转变为 ABC 模式:有 2 种方法。
根据上面的分析,我们可以得出递推公式:
设 $a_i$ 为第 $i$ 行是 ABA模式 的方案数,$b_i$ 为第 $i$ 行是 ABC模式 的方案数。
$$\begin{cases} a_i = 3 \times a_{i-1} + 2 \times b_{i-1} \ b_i = 2 \times a_{i-1} + 2 \times b_{i-1} \end{cases}$$
结果即为 $(a_n + b_n) \pmod{10^9+7}$。
具体代码
func numOfWays(n int) int {
const mod = 1_000_000_007
aba, abc := 6, 6
for range n - 1 {
next_aba := (aba * 3 + abc * 2) % mod
next_abc := (aba * 2 + abc * 2) % mod
aba, abc = next_aba, next_abc
}
return (aba + abc) % mod
}
