题目

给你一棵二叉搜索树，请你返回一棵 平衡后 的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。如果有多种构造方法，请你返回任意一种。

如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是 平衡的 。

示例 1：

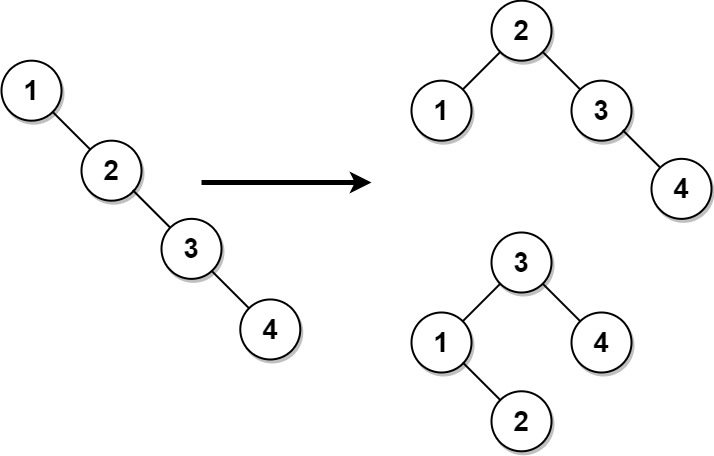
输入：root = [1,null,2,null,3,null,4,null,null] 输出：[2,1,3,null,null,null,4] 解释：这不是唯一的正确答案，[3,1,4,null,2,null,null] 也是一个可行的构造方案。

示例 2：

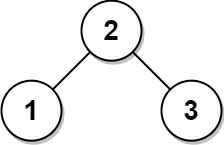
输入: root = [2,1,3] 输出: [2,1,3]

提示：

• 树节点的数目在 [1, 10^4] 范围内。
• 1 <= Node.val <= 10^5

解题思路

解决这道题最通用、最高效的思路是 “归零重启法”，即：先拆后建。

与其尝试在原树上通过复杂的旋转（如 AVL 树或红黑树的左旋右旋）来调整平衡，不如利用二叉搜索树（BST）的特性，将其转化为有序数组，再重新构造一棵完美的平衡二叉搜索树。

第一步：中序遍历（提取有序序列）

二叉搜索树（BST）的一个核心性质是：中序遍历（In-order Traversal）的结果是一个严格递增的有序序列。

不管原树有多“歪”（比如退化成链表），只要我们对其进行中序遍历，就能得到所有节点值的有序排列。

• 输入： 原来的 BST（可能很不平衡）。
• 操作： 递归或迭代进行 左 -> 根 -> 右 遍历。
• 输出： 一个有序数组 nums。

第二步：有序数组构造平衡 BST（分治法）

拿到有序数组后，问题就转化为了：“如何将一个有序数组转换为一棵高度平衡的二叉搜索树”。这其实就是 二分查找 的逆过程。

为了保证树是平衡的（左右子树高度差不超过 1），我们必须让左右子树的节点数量尽可能相等。

• 策略： 总是选择数组的 中间位置（mid） 的元素作为当前的 根节点。
• 递归构造：
  1. 取数组中间元素 nums[mid] 创建根节点。
  2. mid 左边的子数组 nums[left ... mid-1] 递归构造 左子树。
  3. mid 右边的子数组 nums[mid+1 ... right] 递归构造 右子树。
  4. 连接根节点与左右子树。

复杂度分析

• 时间复杂度： $O(N)$
  • 中序遍历需要访问每个节点一次，耗时 $O(N)$。
  • 重建树也需要访问每个数值一次来创建节点，耗时 $O(N)$。
  • 总时间为 $O(N)$。
• 空间复杂度： $O(N)$
  • 我们需要一个数组来存储所有节点的值，占用 $O(N)$ 的空间。
  • 递归构建树时的栈空间为 $O(\log N)$（因为新树是平衡的）。
  • 总空间为 $O(N)$。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def balanceBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        # 1. 中序遍历获取有序数组
        vals = []
        def inorder(node):
            if not node:
                return
            inorder(node.left)
            vals.append(node.val)
            inorder(node.right)
        
        inorder(root)
        
        # 2. 分治法：利用有序数组构建平衡 BST
        def build(left, right):
            if left > right:
                return None
            
            # 总是取中间节点作为根，保证左右高度差最小
            mid = (left + right) // 2
            new_root = TreeNode(vals[mid])
            
            new_root.left = build(left, mid - 1)
            new_root.right = build(mid + 1, right)
            
            return new_root
            
        return build(0, len(vals) - 1)