题目

给你一棵二叉树，它的根为 root 。请你删除 1 条边，使二叉树分裂成两棵子树，且它们子树和的乘积尽可能大。

由于答案可能会很大，请你将结果对 10^9 + 7 取模后再返回。

示例 1：

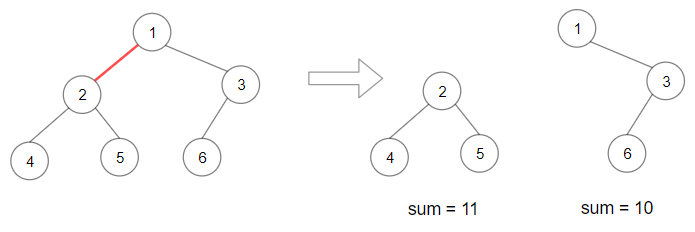
输入：root = [1,2,3,4,5,6] 输出：110 解释：删除红色的边，得到 2 棵子树，和分别为 11 和 10 。它们的乘积是 110 （11*10）

示例 2：

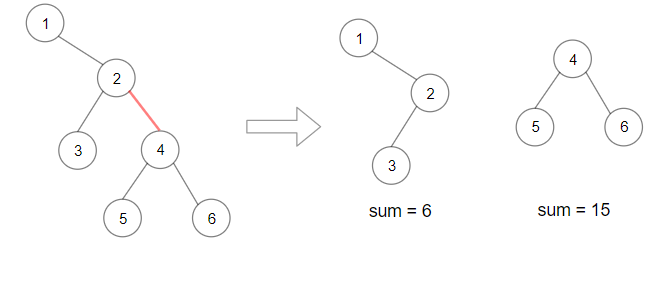
输入：root = [1,null,2,3,4,null,null,5,6] 输出：90 解释：移除红色的边，得到 2 棵子树，和分别是 15 和 6 。它们的乘积为 90 （15*6）

示例 3：

输入：root =[2,3,9,10,7,8,6,5,4,11,1] 输出：1025

示例 4：

输入：root = [1,1] 输出：1

提示：

每棵树最多有 50000 个节点，且至少有 2 个节点。
每个节点的值在 [1, 10000] 之间。

解题思路

这是一个典型“树形 DP（动态规划）” 或者叫 “树上 DFS” 问题。

首先，我们要理解题目中“删除一条边”的物理含义。

物理视角：在一棵树中，连接节点 A（父）和节点 B（子）的边如果被切断，整棵树就会变成两部分：
- 一部分是：以 B 为根的子树。
- 另一部分是：整棵树减去那棵子树。
代数视角：假设整棵树所有节点值的总和是 $S_{total}$。如果我们切断了某个节点 node 上方的边，那么以 node 为根的这棵子树的和记为 $S_{sub}$。那么，剩下的那部分的和必然是：$S_{rest} = S_{total} - S_{sub}$。
目标函数：我们要让这两个数的乘积最大，即最大化：$$P = S_{sub} \times (S_{total} - S_{sub})$$结论：这道题的核心任务变成了算出每一个节点对应的子树和 $S_{sub}$，然后代入公式找最大值。

现在问题变成了：如何快速得到树中每一个节点的子树和？

这需要遍历整棵树。

遍历顺序的选择：就像我们之前讨论的，父亲的子树和依赖于孩子的子树和。
- $Sum_{root} = Sum_{left} + Sum_{right} + Value_{root}$
- 这天然决定了必须使用 后序遍历（Post-order Traversal），即“左右根”或“右左根”的顺序。也就是先深入到底层，算好后一层层向上汇报。
具体操作：我们需要写一个 dfs 函数：
- 输入：一个节点。
- 过程：
  1. 问左孩子要左子树的和。
  2. 问右孩子要右子树的和。
  3. 加上自己的值。
  4. 关键动作：把算出来的这个结果（当前子树和），存到一个列表 all_sums 里备用。
- 返回：把这个和返回给上一层（父节点）。

当 DFS 执行完毕后，我们有了两样东西：

total_sum：整棵树的总和（DFS 遍历根节点的返回值）。
all_sums：一个包含树中所有节点子树和的列表（比如有 50000 个节点，里面就有 50000 个数）。

接下来的逻辑就非常简单了：

遍历列表：拿出 all_sums 里的每一个数 $s$。
代入公式：计算 $current_product = s \times (total_sum - s)$。
擂台法：维护一个 max_product 变量，谁算出来的乘积大，就更新谁。注：从数学直觉上讲，这是在找哪个子树的和最接近 total_sum / 2，因为和固定的两个数，越接近相等，乘积越大。
最后的坑（取模）：题目要求对 $10^9 + 7$ 取模。切记：要在 max_product 完全算出来、比完大小之后，在 return 的那一瞬间再取模。如果在比较过程中取模，会打乱大小关系（例如 $15 > 6$，但模 7 之后 $1 < 6$）。

具体代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxProduct(self, root: Optional[TreeNode]) -> int:
        self.all_sums = []

        # 深度优先搜索 (DFS) 计算子树和
        def dfs(node):
            if not node:
                return 0
            
            # 当前子树和 = 左子树和 + 右子树和 + 当前节点值
            sub_sum = dfs(node.left) + dfs(node.right) + node.val
            
            # 记录这个子树的和
            self.all_sums.append(sub_sum)
            return sub_sum

        # 1. 计算整棵树的总和，并在过程中记录所有子树的和
        total_sum = dfs(root)
        
        max_p = 0
        
        # 2. 遍历每一个子树和，假设断开该子树上面的边
        for s in self.all_sums:
            # 第一部分和是 s，第二部分和是 total_sum - s
            current_p = s * (total_sum - s)
            if current_p > max_p:
                max_p = current_p
        
        # 3. 返回结果对 10^9 + 7 取模
        return max_p % (10**9 + 7)
        
```x

1339. 分裂二叉树的最大乘积

beautifulremi

题目

解题思路

具体代码