题目

给你一个二叉树的根节点 root。设根节点位于二叉树的第 1 层，而根节点的子节点位于第 2 层，依此类推。

返回总和最大的那一层的层号 x。如果有多层的总和一样大，返回其中最小的层号 x。

示例 1：

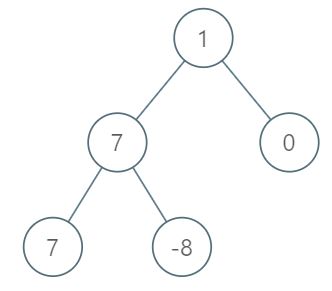
输入：root = [1,7,0,7,-8,null,null] 输出：2 解释：第 1 层各元素之和为 1，第 2 层各元素之和为 7 + 0 = 7，第 3 层各元素之和为 7 + -8 = -1，所以我们返回第 2 层的层号，它的层内元素之和最大。

示例 2：

输入：root = [989,null,10250,98693,-89388,null,null,null,-32127] 输出：2

提示：

树中的节点数在 [1, 104]范围内
-10^5 <= Node.val <= 10^5

解题思路

我们要找到“哪一层”的所有数字加起来最大。如果有两层的总和一样大，我们要那个层号更小（更靠近根部）的。这就需要用到“广度优先搜索 (BFS)”，也就是层序遍历。

第一步：初始化

第1层只有一个人（根节点）。
不管是多少人，先把他们赶到一个**“等待室”（队列）**里去。

第二步：锁定当前层人数（这是最重要的一步！）

这是很多初学者容易晕的地方。

当你要开始处理第 X 层时，你先看一眼“等待室”里现在有几个人？假设有 N 个人。
这 N 个人，就是第 X 层的所有成员。
死命令：你接下来只准处理这 N 个人，多一个都不行！因为后来再进等待室的，那都是第 X+1 层（下一层）的人了。

第三步：算账 + 安排下一代

现在开始处理这 N 个人（写个循环，跑 N 次）：

把人从等待室叫出来。
把他身上的钱（节点值）加到**“当前层总账”**里。
问他：“你有孩子吗？（左节点/右节点）”。
如果有孩子，把孩子赶进“等待室”的队尾排队去。

第四步：比大小

这 N 个人处理完了（循环结束了）：

看一眼**“当前层总账”**。
如果比你之前记录的**“历史最大账”**还要大：
- 好，更新“历史最大账”。
- 记下现在的层号（比如现在是第 2 层）。
注意：如果和历史最大账一样大，不要更新，因为我们要保住那个层号更小的记录。

第五步：进入下一层

现在的层号 +1。
回到第二步，继续看“等待室”里现在有多少人（这些都是刚才那波人的孩子）。

具体代码

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxLevelSum(root *TreeNode) int {
    // 初始化最大和为最小值 (Go int 最小值)
    // 也可以初始化为 root.Val，因为题目保证树不为空
    maxSum := -1 << 63 
    ansLevel, currLevel := 1, 1
    
    queue := []*TreeNode{root}
    
    for len(queue) > 0 {
        size := len(queue)
        levelSum := 0
        
        for i := 0; i < size; i++ {
            node := queue[0]
            queue = queue[1:] // 出队
            
            levelSum += node.Val
            
            if node.Left != nil {
                queue = append(queue, node.Left)
            }
            if node.Right != nil {
                queue = append(queue, node.Right)
            }
        }
        
        // 如果当前层和大于记录的最大值，则更新
        if levelSum > maxSum {
            maxSum = levelSum
            ansLevel = currLevel
        }
        
        currLevel++
    }
    
    return ansLevel
}

1161. 最大层内元素和

beautifulremi

题目