题目

你有一个凸的 n 边形，其每个顶点都有一个整数值。给定一个整数数组 values ，其中 values[i] 是第 i 个顶点的值（即 顺时针顺序 ）。

假设将多边形剖分为 n - 2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。

返回 多边形进行三角剖分后可以得到的最低分 。

示例 1：

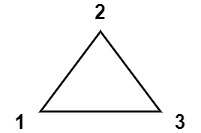
输入：values = [1,2,3] 输出：6 解释：多边形已经三角化，唯一三角形的分数为 6。

示例 2：

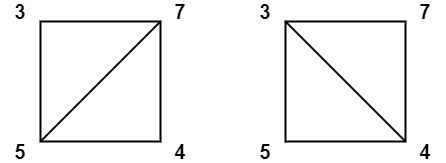
输入：values = [3,7,4,5] 输出：144 解释：有两种三角剖分，可能得分分别为：3*7*5 + 4*5*7 = 245，或 3*4*5 + 3*4*7 = 144。最低分数为 144。

示例 3：

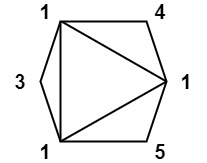
输入：values = [1,3,1,4,1,5] 输出：13 解释：最低分数三角剖分的得分情况为 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13。

提示：

n == values.length
3 <= n <= 50
1 <= values[i] <= 100

解题思路

核心思想是：通过解决小多边形的三角剖分问题，来逐步构建出大多边形的最优解。

下面我们来分解这个思路：

1. 定义子问题

首先，我们要定义一个子问题。原问题是求解整个n边形（顶点 0 到 n-1）的最低分数。我们可以将其缩小为：

计算由顶点 i 到顶点 j (顺时针) 构成的子多边形的最低三角剖分分数。

我们用 dp[i][j] 来表示这个值。dp[i][j] 的含义是：对顶点 values[i], values[i+1], ..., values[j] 构成的子多边形进行三角剖分，可以得到的最低分数。

我们的最终目标就是求解 dp[0][n-1]。

2. 状态转移方程（核心）

现在，我们如何从更小的子问题来计算 dp[i][j] 呢？

考虑由顶点 i 到 j 构成的子多边形。在任何一种三角剖分中，边 (i, j) 必然会与某个中间顶点 k (其中 i < k < j) 形成一个三角形 (i, k, j)。

当我们固定这个三角形 (i, k, j) 后，会发生什么？

这个三角形自身的分数是 values[i] * values[k] * values[j]。
原来的子多边形被这个三角形分成了两个更小的子多边形（如果它们存在的话）：
- 一个是由顶点 i 到 k 构成的子多边形。它的最低剖分分数是 dp[i][k]。
- 另一个是由顶点 k 到 j 构成的子多边形。它的最低剖分分数是 dp[k][j]。

因此，如果我们选择顶点 k 作为连接边 (i, j) 的那个点，那么总分数就是： dp[i][k] + dp[k][j] + values[i] * values[k] * values[j]

为了得到 dp[i][j] 的最低分数，我们必须遍历所有可能的中间点 k (从 i+1 到 j-1)，然后取其中的最小值。

这就得到了我们的状态转移方程:

$$dp[i][j]=\min_{i<k<j}{dp[i][k]+dp[k][j]+\mathrm{values}[i]\times\mathrm{values}[k]\times\mathrm{values}[j]}$$

3. 基本情况（Base Case）

状态转移方程依赖于更小的子问题。那么最小的子问题是什么？

dp[i][j] 的定义是剖分一个由 j - i + 1 个顶点组成的多边形。一个多边形至少需要3个顶点才能形成三角形。

如果只有两个顶点（例如 i 和 i+1），它们只构成一条边，无法形成三角形。因此，剖分的分数为 0。
所以，当 j == i + 1 时，dp[i][i+1] = 0。这就是我们的基本情况。

4. 计算顺序

为了确保在计算 dp[i][j] 时，所有它依赖的更小的子问题 dp[i][k] 和 dp[k][j] 都已经被计算出来了，我们需要按照子多边形 由短到长 的顺序来计算。

我们可以用多边形的“跨度”（或长度） len 来控制计算顺序，len 表示多边形包含的顶点数。

len = 1 或 2：无法形成三角形，分数为0。
len = 3：这是最小的多边形，即三角形。例如 dp[i][i+2]。它只能形成一个三角形 (i, i+1, i+2)。
- k 只能取 i+1。
- dp[i][i+2] = dp[i][i+1] + dp[i+1][i+2] + values[i]*values[i+1]*values[i+2]
- 根据基本情况，dp[i][i+1] 和 dp[i+1][i+2] 都为0。
- 所以 dp[i][i+2] = values[i] * values[i+1] * values[i+2]。
len = 4：例如 dp[i][i+3]，可以被剖分成两个三角形。
...
len = n：最后计算 dp[0][n-1]。

这个过程可以通过一个嵌套循环来实现：

外层循环遍历跨度 len，从 3 到 n。
内层循环遍历起始点 i。
根据 len 和 i 计算出终点 j = i + len - 1。
最内层循环遍历 k (从 i+1 到 j-1)，根据状态转移方程计算 dp[i][j] 的最小值。

总结解题步骤

创建一个 n x n 的二维数组 dp，用于存储子问题的解。
初始化 dp 数组。虽然基本情况是 dp[i][i+1] = 0，但通常将整个数组初始化为0即可。
按跨度 len 从 3 到 n 进行迭代。
在每个跨度内，迭代所有可能的起始顶点 i (从 0 到 n-len)。
计算终点 j = i + len - 1。
初始化 dp[i][j] 为一个非常大的数（正无穷）。
迭代所有可能的中间顶点 k (从 i+1 到 j-1)，应用状态转移方程更新 dp[i][j] 为更小的值。
所有循环结束后，dp[0][n-1] 就是最终答案。

时间复杂度

时间复杂度：$O(n^3)$

这个复杂度主要来自于填充 dp 表所需的三层嵌套循环：

第一层循环（跨度 len）：遍历所有可能的子多-边形长度，从 3 到 n。这个循环大约执行 n 次。
- for (len = 3; len <= n; len++)
第二层循环（起始点 i）：对于每个长度，遍历所有可能的起始顶点 i。这个循环也大约执行 n 次。
- for (i = 0; i <= n - len; i++)
第三层循环（分割点 k）：对于每个子多边形 (i, j)，需要遍历所有可能的中间顶点 k 来寻找最优分割点。k的范围是从 i+1 到 j-1，其长度 j-i-1 与 len 成正比。因此，这个循环也大约执行 n 次。
- for (k = i + 1; k < j; k++)

由于这三层循环是嵌套的，总的操作次数大约是 n×n×n，所以时间复杂度为 $O(n^3)$。

具体代码

func minScoreTriangulation(values []int) int {
    n := len(values)

    // dp[i][j] 表示由顶点 i, i+1, ..., j 构成的子多边形进行三角剖分的最低分
    dp := make([][]int, n)
    for i := range dp {
        dp[i] = make([]int, n)
    }

    // len 是子多边形的顶点数
    // 从最小的三角形（len=3）开始计算，逐步扩大到整个多边形（len=n）
    for length := 3; length <= n; length++ {
        // i 是子多边形的起始顶点
        for i := 0; i <= n-length; i++ {
            // j 是子多边形的结束顶点
            j := i + length - 1

            // 初始化 dp[i][j] 为一个极大值，方便后续取最小值
            dp[i][j] = math.MaxInt32

            // k 是边 (i, j) 与之构成三角形的中间顶点
            // 遍历所有可能的 k，找到最优的分割点
            for k := i + 1; k < j; k++ {
                // 应用状态转移方程
                score := dp[i][k] + dp[k][j] + values[i]*values[k]*values[j]
                
                // 更新为更小的值
                if score < dp[i][j] {
                    dp[i][j] = score
                }
            }
        }
    }

    // dp[0][n-1] 存储了整个多边形（从顶点 0 到 n-1）的最低分
    return dp[0][n-1]
}

1039. 多边形三角剖分的最低得分

beautifulremi

题目